Trên đường thẳng y = 2 x + 1 có bao nhiêu điểm kẻ được đến đồ thị (C) hàm số x + 3 x - 1 đúng một tiếp tuyến?
A. 4
B. 3
C. 2
D. 1
Cho hàm số y= x3-6x2+9x-1 có đồ thị là (C) . Từ một điểm bất kì trên đường thẳng x=2 kẻ được bao nhiêu tiếp tuyến đến (C)
A.2
B.1
C.3
D.0
+ Xét đường thẳng kẻ từ một điểm bất kì trên đường thẳng x= 2 có dạng:
∆: y= k( x-2) hay y= kx-2k
+ ∆ là tiếp tuyến của (C)
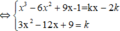
có nghiệm

+ Phương trình bậc ba có duy nhất một nghiệm tương ứng cho ta một giá trị k . Vậy có một tiếp tuyến.
+ Dễ thấy kẻ từ một điểm bất kì trên đường thẳng x=2có dạng y= a song song với trục Ox cũng chỉ kẻ được một tiếp tuyến.
Chọn B.
Trên đường thẳng y = 2 x + 1 có bao nhiêu điểm mà từ đó kẻ được đúng một tiếp tuyến đến đồ thị của hàm số y = x + 3 x − 1
A. 2
B. 4
C. 1
D. 3
Đáp án A
Ta có: y ' = x − 1 − x + 3 x − 1 2 = − 4 x − 1 2 .
Tiếp tuyến tại M x 0 ; x 0 + 3 x 0 − 1 ∈ C là:
y = − 4 x 0 − 1 2 x − x 0 + x 0 + 3 x 0 − 1 = − 4 x x 0 − 1 2 + x 0 2 + 6 x 0 − 3 x 0 − 1 2 .
Tiếp tuyến đi qua M x 1 ; 2 x 1 + 1 nên:
2 x 1 + 1 = − 4 x 1 x 0 − 1 2 + x 0 2 + 6 x 0 − 3 x 0 − 1 2
⇔ 2 x 1 + 1 x 0 2 − 2 x 0 + 1 = x 0 2 + 6 x 0 − 3 − 4 x 1 ⇔ 2 x 1 − 1 x 0 2 − 4 x 1 + 2 x 0 + 6 x 1 + 4 = 0 (*)
Qua M x 1 ; 2 x 1 + 1 kẻ được đúng một tiếp tuyến đến đồ thị hàm số (C) nên (*) có nghiệm duy nhất
⇔ Δ ' = 4 x 1 + 2 2 − 2 x 1 − 1 6 x 1 + 4 = 0 ⇔ − 4 x 1 2 + 7 x 1 + 10 = 0 ⇔ x 1 = 7 ± 209 8 .
Vậy có 2 điểm từ đó kẻ được đúng 1 tiếp tuyến đến đồ thị hàm số.
Cho hàm số y = x 3 − 3 x + 2 có đồ thị (C). Hỏi có bao nhiêu điểm trên đường thẳng y = 9 x − 14 sao cho từ đó kẻ được hai tiếp tuyến đến (C).
A. 4 điểm
B. 2 điểm
C. 3 điểm
D. 1 điểm
Đáp án C
Phương pháp:
Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
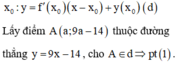
Để từ A kẻ được hai tiếp tuyến đến (C) thì phương trình (1) có 2 nghiệm phân biệt. Tìm điều kiện của a để phương trình có 2 nghiệm phân biệt. Có bao nhiêu giá trị của a thì có bấy nhiêu điểm thỏa mãn yêu cầu bài toán.

Cách giải:
TXĐ : D = R.
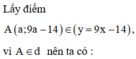
9 a − 14 = 3 x 0 2 − 3 a − x 0 + x 0 3 − 3 x 0 + 2 1
⇔ 9 a − 14 = 3 a x 0 2 − 3 x 0 3 − 3 a + 3 x 0 + x 0 3 − 3 x 0 + 2
⇔ − 2 x 0 3 + 3 a x 0 2 − 12 a + 16 = 0
⇔ x 0 − 2 − 2 x 0 2 + 3 a − 4 x 0 + 6 a − 8 = 0
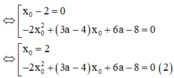
Để qua A kẻ được 2 tiếp tuyến đến đồ thị (C) thì phương trình (1) có 2 nghiệm phân biệt.
TH1 : x 0 = 2 là nghiệm của phương trình (2) ta có :

TH2 : x 0 = 2 không là nghiệm của phương trình (2), khi đó để (1) có 2 nghiệm phân biệt thì (2) có nghiệm kép khác 2.
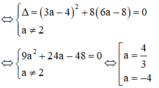
Vậy có 3 giá trị của a thỏa mãn yêu cầu bài toán.
Chú ý và sai lầm: Cần phải làm hết các trường hợp để phương trình (1) có 2 nghiệm, tránh trường hợp thiếu TH1 và chọn nhầm đáp án B.
Cho hàm số y = x 3 - 3 x + 2 có đồ thị (C). Hỏi có bao nhiêu điểm trên đường thẳng d: y = 9x-14 sao cho từ đó kẻ được 2 tiếp tuyến đến (C).
A. 4 điểm
B. 2 điểm
C. 1 điểm
D. 3 điểm
Đáp án D
A ∈ d ⇒ A a ; 9 a - 14
Pt tiếp tuyến qua A y = k(x-a)+9a-14
Qua A kẻ được 2 tiếp tuyến khi và chỉ khi hpt sau có 2 nghiệm:
k ( x - a ) + 9 a - 14 = x 3 - 3 x + 2 ( 1 ) k = 3 x 2 - 3 ( 2 )
Thay (2) vào (1) ta được:
3 x 2 - 3 x - a + 9 a - 14 = x 3 - 3 x + 12 ⇔ 3 x 3 - 3 a x 2 - 3 x + 12 a - 14 = x 3 - 3 x + 12 ⇔ x - 2 2 x 2 + - 3 a + 4 x - 6 a + 8 = 0 ⇔ [ x = 2 2 x 2 + - 3 a + 4 x - 6 a + 8 = 0 2 x 2 + - 3 a + 4 x - 6 a + 8 = 0 ∆ = 9 a 2 + 24 a - 48
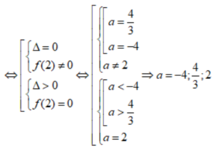
Cho hàm số y = x 3 − 3 x + 2 có đồ thị (C). Hỏi có bao nhiêu điểm trên đường thẳng d: y = 9x - 14 sao cho từ đó kẻ được 2 tiếp tuyến đến (C)?
A. 4 điểm
B. 2 điểm
C. 1 điểm
D. 3 điểm
Đáp án D
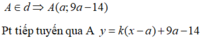
Qua A kẻ được 2 tiếp tuyến khi và chỉ khi hpt sau có 2 nghiệm:
Có bao nhiêu điểm có toạ độ nguyên nằm trên đường thẳng x=2 kẻ được ít nhất hai tiếp tuyến tới đồ thị hàm số y = x 3 - 3 x .
A. 7.
B. 3.
C. 9.
D. 8.
Có bao nhiêu điểm có toạ độ nguyên nằm trên đường thẳng x = 2 kẻ được ít nhất hai tiếp tuyến tới đồ thị hàm số y = x 3 - 3 x .
A. 7.
B. 3.
C. 9.
D. 8.
Cho hàm số y = x 3 - 5 x 2 có đồ thị (C). Hỏi có bao nhiêu điểm trên đường thẳng d : y = 2 x - 6 sao cho từ đó kẻ được đúng hai tiếp tuyến đến (C)?
A. 2 điểm
B. 3 điểm
C. 4 điểm
D. vô số điểm
Cho hàm số y = x 3 − 6 x 2 + 9 x − 1 có đồ thị là (C). Gọi T là tập hợp tất cả các điểm thuộc đường thẳng y=x-1 mà từ điểm đó kẻ được đúng 2 tiếp tuyến đến đồ thị (C). Tìm tổng tung độ của các điểm thuộc T.
A. ‒1
B. 0
C. 1
D. 2