Một khối trụ có chiều cao bằng 3cm , bán kính đáy bằng 1cm có thể tích bằng

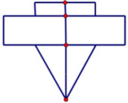
Một con quay là ghép của 2 khối trụ được xếp chồng lên khối nón. Thiết diện qua trục có dạng như hình vẽ bên. Khối trụ thứ nhất có bán kính đáy r1, chiều cao h1; khối trụ thứ hai có bán kính đáy r2, chiều cao h2; khối nón có bán kính đáy r3, chiều cao h3. Biết rằng r2 = 2r1 = 2r3; h3 = 2h2 = 4h1 và thể tích của con quay bằng 31 c m cubed Thể tích của phần khối nón bằng

A.  3 c m 3

B.  6 c m 3

C.  8 c m 3

D.  4 c m 3

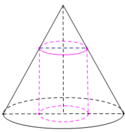
Cho hình nón có bán kính đáy bằng 3 chiều cao bằng 6, một khối trụ có bán kính đáy thay đổi nội tiếp khối nón đã cho (như hình vẽ). Thể tích lớn nhất của khối trụ bằng:

A.  6 π

B.  10 π

C.  4 π

D.  8 π

Một khối trụ có thể tích bằng 25 π . Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì khối trụ mới có diện tích xung quanh bằng 25. Bán kính đáy của khối trụ ban đầu là:

A.  r = 10

B.  r = 5

C. r = 2

D.  r = 15

Cho khối trụ có bán kính đáy bằng a và chiều cao bằng  3 a . Thể tích của khối trụ bằng