Khẳng đỉnh nào sau đây là sai?
A. Có một mặt cầu đi qua các đỉnh của một tứ diện bất kì.
B. Có một mặt cầu đi qua các đỉnh của một hình lăng trụ có đáy là một tứ giác lồi.
C. Có một mặt cầu đi qua các đỉnh của một hình hộp chữ nhật.
D. Có một mặt cầu đi qua các đỉnh của một hình chóp đều.
Chọn B.
Nếu có một mặt cầu ngoại tiếp lăng trụ thì đáy của lăng trụ phải nội tiếp trong một đường tròn, điều này không đúng cho tứ giác lồi bất kì.
Hỏi hình tạo bởi 6 đỉnh là 6 trung điểm của các cạnh một tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A. 6
B. 3
C. 4
D. 9
Phương pháp:
Sử dụng lý thuyết khối đa diện để làm bài toán.
Cách giải:
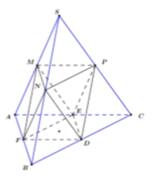
Khối đa diện được tạo từ 6 đỉnh là 6 trung điểm của các cạnh của tứ diện đều là khối bát diện đều có 6 đỉnh, 12 cạnh và 8 mặt.
Khối bát diện đều là khối đa diện có 9 mặt đối xứng.
Chọn: D
Tính thể tích V của khối nón ngoại tiếp hình tứ diện đều có cạnh bằng a (khối nón có đỉnh là một đỉnh của tứ diện và có đáy là hình tròn đi qua 3 đỉnh còn lại của tứ diện).
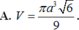
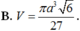
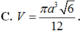
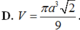
Tính thể tích V của khối nón ngoại tiếp hình tứ diện đều có cạnh bằng a (khối nón có đỉnh là một đỉnh của tứ diện và có đáy là hình tròn đi qua 3 đỉnh còn lại của tứ diện).
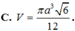
tính diện tích toàn phần của hình chóp tứ giác đều có cạnh đáy 25m và chiều cao mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 20cm
20 cm = 0,2 m
Diện tích toàn phần của hình chóp tứ giác đều là:
\(\dfrac12\cdot(4\cdot25)\cdot0,2+25^2=635(m^2)\)
Vậy: ...
\(\text{#}Toru\)
Tính diện tích toàn phần của hình chóp tứ giác đều có cạnh đáy 25m và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 20m
Sxq=1/2*24*4*20=12*80=960m2
Stp=960+25^2=1585m2
Một hình tứ diện đều có cạnh a có một đỉnh trùng với đỉnh của hình nón tròn xoay còn ba đỉnh còn lại của tứ diện nằm trên đường tròn đáy của hình nón. Diện tích xung quanh của hình nón là:
A. 1 3 π a 2 3
B. π a 2 2
C. 1 3 π a 2 2
D. 1 2 π a 2 3
Một hình tứ diện đều có cạnh a có một đỉnh trùng với đỉnh của hình nón tròn xoay còn ba đỉnh còn lại của tứ diện nằm trên đường tròn đáy của hình nón. Diện tích xung quanh của hình nón là:
A. 1 3 πa 2 3
B. πa 2 2
C. 1 3 πa 2 2
D. 1 2 πa 2 3
Trong một hình tứ diện ta tô màu các đỉnh, trung điểm các cạnh, trọng tâm các mặt và trọng tâm tứ diện. Chọn ngẫu nhiên 4 điểm trong số các điểm đã tô màu. Tính xác suất để 4 điểm được chọn là 4 đỉnh của một hình tứ diện.
A. 188 273
B. 1009 1365
C. 245 273
D. 136 195
Đáp án A.
Có tất cả 15 điểm được tô màu gồm 4 đỉnh của tứ diện, 6 trung điểm của 6 cạnh, 4 trọng tâm của 4 mặt bên và 1 trọng tâm của tứ diện.
Không gian mẫu là “Chọn ngẫu nhiên 4 trong số 15 điểm đã tô màu”. Số phần tử của không gian mẫu là n Ω = C 15 4 .
Gọi A là biến cố “4 điểm được chọn đồng phẳng”. Suy ra là biến cố “4 điểm được chọn là 4 đỉnh của một hình tứ diện”. Để xác định số kết quả thuận lợi cho biến cố A ta xét các trường hợp sau:
a. 4 điểm cùng thuộc “một mặt bên của tứ diện”
Một mặt bên có 7 điểm được tô màu nên số cách chọn 4 điểm (đồng phẳng) trên một mặt bên là C 7 4 (cách).
Có tất cả 4 mặt bên nên số cách chọn thỏa mãn trường hợp a. là 4. C 7 4 (cách).
b. 4 điểm cùng thuộc mặt phẳng “chứa 1 cạnh của tứ diện và trung điểm của cạnh đối diện:.
Mặt phẳng đó có 7 điểm được tô màu nên số cách chọn 4 điểm (đồng phẳng) trên mỗi mặt là C 7 4 (cách).
Hình tứ diện có 6 cạnh nên có tất cả 6 mặt như thế. Số cách chọn 4 điểm thỏa mãn trường hợp b. là 6 C 7 4 (cách).
c. 4 điểm cùng thuộc mặt phẳng “chứa 1 đỉnh và đường trung bình của tam giác đối diện đỉnh đó”.
Mặt phẳng đó có 5 điểm được tô màu nên số cách chọn 4 điểm (đồng phẳng) trên mỗi mặt là C 5 4 (cách).
Do mỗi mặt bên là một tam giác có 3 đường trung bình, nên mỗi đỉnh có tương ứng 3 mặt phẳng như thế (chứa đỉnh và đường trung bình). Mà tứ diện có 4 đỉnh nên có tất cả 3.4 = 12 mặt phẳng ở trường hợp c.
Vậy số cách chọn thỏa mãn trường hợp c. là 12 C 5 4 (cách).
d. 4 điểm cùng thuộc mặt phẳng “chứa 2 đường nối 2 trung điểm của các cạnh đối diện”.
Có 3 đường nối 2 trung điểm của các cạnh đối diện. Số mặt phẳng được tạo thành từ 2 trong 3 đường đó là C 3 2 (mặt phẳng).
Mỗi mặt phẳng như thế có 5 điểm được tô màu nên số cách chọn 4 điểm (đồng phẳng) là C 5 4 (cách).
Vậy số cách chọn thỏa mãn trường hợp d. là C 3 2 . C 5 4 (cách).
Số kết quả thuận lợi cho biến cố A là n A = 4 C 7 4 + 6 C 7 4 + 12 C 5 4 + C 3 2 . C 5 4 = 425 .
Vậy xác suất cần tính là
P A ¯ = 1 − P A = 1 − n A n Ω = 1 − 425 C 15 4 = 188 173
Một hình tứ diện đều cạnh a có một đỉnh trùng với đỉnh của hình nón tròn xoay còn ba đỉnh còn lại của tứ diện nằm trên đường tròn đáy của hình nón. Diện tích xung quanh của hình nón tròn xoay là:
A. 1 3 πa 2 3 B. πa 2 2
C. 1 3 πa 2 2 D. 1 2 πa 2 3
