Tính tổng bình phương giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 4 + 4 x 2 + 3 trên đoạn - 1 ; 1 ?
A. 121
B. 64
C. 73
D. 22
Tổng bình phương giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + 1 x 2 + 1 trên đoạn [0;3] là
A. 3
B. 2
C. 5
D. 4
Gọi M và m lần lượt là giá trị nhỏ nhất và giá trị lớn nhất cùa hàm số \(y=\frac{x^2+8x+7}{x^2+1},x\in[-3;2]\) .Tính tổng bình phương của M và m
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x − 4 − x 2 . Tính tổng M + m.
A. M + m = 2 − 2
B. M + m = 2 1 + 2
C. M + m = 2 1 − 2
D. M + m = 4
Chọn C.
Phương pháp:
+) Tìm tập xác định D = [a;b] của hàm số đã cho.

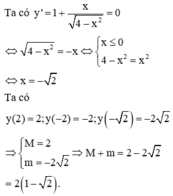
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x - 4 - x 2 Tính tổng M+m
A. 2 - 2
B. 2 1 + 2
C. 2 1 - 2
D. 4
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x - 4 - x 2 . Tính tổng M + m.
A. M + m = 2 - 2
B. M + m = 2(1 + 2 )
C. M + m = 2(1 - 2 )
D. M + m = 4
Chọn C
Tập xác định: ![]()
![]()
![]()
Do đó ![]()
Chọn đáp án C
Tổng bình phương giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 3 - 3 x + 2 trên đoạn [0;2] là
A. 4
B. 2
C. 16
D. 2
Đáp án C
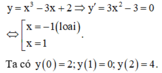
Vậy tổng bình phương giá trị lớn nhất và giá trị nhỏ nhất là 16.
Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 3 + 3 x 2 − 12 x + 2 trên đoạn [-1;2]. Tính tổng bình phương của M và m.
A. 100
B. 225
C. 250
D. 200
Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
\(y=x^3-3x^2-9x+35\) trên các đoạn [-4; 4] và [0;5] ;
\(y'=3x^2-6x-9=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
a. Trên [-4;4] ta có:
\(y\left(-4\right)=-41\) ; \(y\left(-1\right)=40\) ; \(y\left(3\right)=8\) ; \(y\left(4\right)=15\)
\(\Rightarrow y_{min}=-41\) ; \(y_{max}=40\)
b. Trên [0;5] ta có:
\(y\left(0\right)=35\) ; \(y\left(3\right)=8\); \(y\left(5\right)=40\)
\(\Rightarrow y_{max}=40\) ; \(y_{min}=8\)
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 - x 2 - x là
A. 2- 2 .
B. 2.
C. 2+ 2 .
D. 1.