Đáp án C
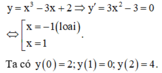
Vậy tổng bình phương giá trị lớn nhất và giá trị nhỏ nhất là 16.
Đáp án C
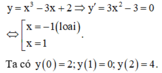
Vậy tổng bình phương giá trị lớn nhất và giá trị nhỏ nhất là 16.
Tổng bình phương giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + 1 x 2 + 1 trên đoạn [0;3] là
A. 3
B. 2
C. 5
D. 4
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = - 2 x 4 + 4 x 2 + 3 trên đoạn [0;2] lần lượt là
A. 6 và -12
B. 6 và -13
C. 5 và -13
D. 6 và -31
Ký hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [ 0;2]. Giá trị a+ A bằng
A. 7
B. 18
C. 0
D. 12
Kí hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn 0 ; 2 . Khi đó giá trị của a + A bằng:
A. 7
B. 18
C. 0
D. 12
Tính tổng bình phương giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 4 + 4 x 2 + 3 trên đoạn - 1 ; 1 ?
A. 121
B. 64
C. 73
D. 22
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 3 + 3 x 2 − 12 x + 2 trên đoạn − 1 ; 2 . Tìm tổng bình phương của M và m
A. 250.
B. 100.
C. 509.
D. 289.
Gọi m là giá trị nhỏ nhất và M là giá trị lớn nhất của hàm số y = x 4 - 2 x 2 - 3 trên đoạn 0 ; 2 . Giá trị biểu thức M + m bằng
A. 2.
B. 1
C. -3.
D. -7.
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 4 - 2 x 2 + 3 trên đoạn [0;2]. Tính giá trị của biểu thức M+2m.
A. M+2m=13.
B. M+2m=5.
C. M+2m=14.
D. M+2m=15.
Giá trị lớn nhất của hàm số y = x − 1 x + 2 trên đoạn [0;2]là:
A. 1/4
B. 2
C. - 1/2
D. 0