Cho hàm số y=f(x) liên tục trên tập Rvà có đồ thị (C) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình f 2 ( x ) - ( m - 1 ) f ( x ) + m - 2  có 12 nghiệm phân biệt?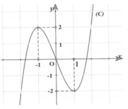

Cho đồ thị hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 100 ) + m 2  có 5 điểm cực trị? 

A. 0.

B. 1.

C. 2.

D. 4.

Có bao nhiêu giá trị m nguyên để đồ thị hàm số y = x - 2 x 2 - m x + m  có đúng một tiệm cận đứng

A. 1

B. 2

C. 3

D. 4

Cho đồ thị hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f x + 100 + m 2 có 5 điểm cực trị?

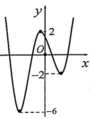
A. 0

B. 1

C. 2

D. 4

Có tất cả bao nhiêu số nguyên m để đồ thị hàm số y = x + m x 2 + x + 1  có đường tiệm cận ngang?

A. 1. 

B. 2.  

C. 0.  

D. vô số.

Cho hàm số y=f(x) liên tục trên tập  ℝ   và có đồ thị (C) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để phương trình f 2 x - m - 1 f x + m - 2 = 0  có 12 nghiệm phân biệt?

A. Không tồn tại m

B. 1

C. 2

D. 3