Cho hình chóp S.ABC có đáy ABC là tam giác cân tại C , S A B ⊥ A B C , S A = S B , I là trung điểm AB Góc giữa đường thẳng SC và mặt phẳng (ABC) là:
A. Góc S C I ⏜
B. Góc S C A ⏜
C. Góc I S C ⏜
D. Góc S C B ⏜
Những câu hỏi liên quan
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450. A.
a
3
3
4
B.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Đáp án C
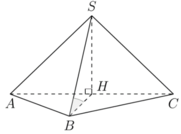
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450 A.
a
3
3
4
B.
a
3
3
12...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC2a. Mặt bên SBC là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABC là
A
.
V
a
3
B
.
V
2
a
3
3
C
.
V...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC=2a. Mặt bên SBC là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABC là
A . V = a 3
B . V = 2 a 3 3
C . V = 2 a 3 3
D . a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB AC a; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC A.
1
12
a
3
B.
3
4
a
3
C.
3
12...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB = AC= a; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC
A. 1 12 a 3
B. 3 4 a 3
C. 3 12 a 3
D. 1 4 a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân,
A
B
A
C
a
; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC. A.
1
12
a
3
B.
3
4
a
3
C. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, A B = A C = a ; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC.
A. 1 12 a 3
B. 3 4 a 3
C. 3 12 a 3
D. 1 4 a 3
Đáp án A
Gọi H là trung điểm của AB suy ra S H ⊥ A B
Do Δ S A B vuông cân tại S nên S H = A B 2 = a 2 ; S A B C = a 2 2 ⇒ V = a 3 12 .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và ABACa, biết tam giác cân SAB cân tại S và nằm trong mặt phẳng vuông góc với (ABC). Mặt phẳng (SAC) hợp với mặt phẳng (ABC) một góc bằng . Thể tích của khối chóp S.ABC bằng A.
a
3
3
B.
a
3
4
C.
a
3
9
D. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB=AC=a, biết tam giác cân SAB cân tại S và nằm trong mặt phẳng vuông góc với (ABC). Mặt phẳng (SAC) hợp với mặt phẳng (ABC) một góc bằng . Thể tích của khối chóp S.ABC bằng
A. a 3 3
B. a 3 4
C. a 3 9
D. a 3 12
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 17:40
Cho hình chóp S.ABC có đáy là tam giác cân tại A và SA \( \bot \) (ABC). Gọi M là trung điểm của BC. Chứng minh rằng:
a) BC \( \bot \) (SAM);
b) Tam giác SBC cân tại S.
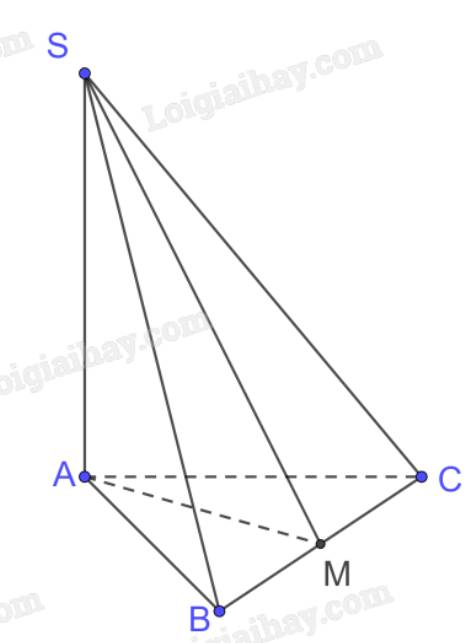
a) Xét tam giác ABC cân tại A có
AM là đường trung tuyến (M là trung điểm BC)
\( \Rightarrow \) AM là đường cao \( \Rightarrow \) \(AM \bot BC\)
Ta có:
\(\left. \begin{array}{l}AM \bot BC\\SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right)\\AM \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAM} \right)\)
b) \(\left. \begin{array}{l}BC \bot \left( {SAM} \right)\\SM \subset \left( {SAM} \right)\end{array} \right\} \Rightarrow BC \bot SM\)
Xét tam giác SBC có:
+) SM là đường cao \(\left( {BC \bot SM} \right)\)
+) SM là đường trung tuyến (M là trung điểm BC)
\( \Rightarrow \) Tam giác SBC cân tại S.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt phẳng (SAB) vuông góc với mặt phẳng (ABC) và tam giác SAB vuông cân tại S. Tính thể tích khối chóp S.ABC theo a
A
.
a
3
3
12
B
.
a
3
3
24...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt phẳng (SAB) vuông góc với mặt phẳng (ABC) và tam giác SAB vuông cân tại S. Tính thể tích khối chóp S.ABC theo a
A . a 3 3 12
B . a 3 3 24
C . a 3 3 3
D . a 3 3 4
Đáp án B
Vì tam giác SAB cân tại S nên hạ SH ⊥ AB => H là trung điểm của AB.
Vì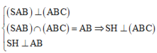 
Tam giác SAB vuông cân tại S nên SA = SB = a 2
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B,
A
B
a
;
S
A
2
a
;
S
A
⊥
A
B
C
. Bán kính của mặt cầu ngoại tiếp hình chóp S.ABC là: A.
a
6
2
...
Đọc tiếp
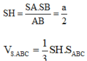
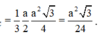
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, A B = a ; S A = 2 a ; S A ⊥ A B C . Bán kính của mặt cầu ngoại tiếp hình chóp S.ABC là:
A. a 6 2
B. a 6 6
C. a 3 2
D. a 6 3
Gọi O, I lần lượt là trung điểm của AC, SC.
Ta có:
∆ A B C vuông cân tại B ⇒ O là tâm đường tròn ngoại tiếp và A C = A B 2 = a 2 .
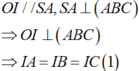
∆ S A C vuông tại A, I là trung điểm của S C ⇒ I S = I C = I A 2
Từ (1), (2) suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABC, bán kính
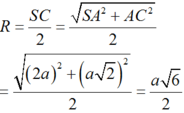
Chọn: A
Đúng 0
Bình luận (0)
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB BC a cạnh bên SA vuông góc với đáy và SA a. Tính diện tích toàn phần
S
t
p
của hình chóp S.ABC. A.
S
t
p
2
a
2
B.
S
t
p
a...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = a cạnh bên SA vuông góc với đáy và SA = a. Tính diện tích toàn phần S t p của hình chóp S.ABC.
A. S t p = 2 a 2
B. S t p = a 2 1 + 2
C. S t p = a 2 1 + 2 2
D. S t p = 2 a 2 2