Trong không gian Oxyz, cho các điểm A 0 ; 4 2 ; 0 , B 0 , 0 , 4 2 điểm C ∈ m p O x y và tam giác OAC vuông tại C; hình chiếu vuông góc của O trên BC là điểm H. Khi đó điểm H luôn thuộc đường tròn cố định có bán kính bằng:
A. 2 2
B. 4
C. 3
D. 2
Những câu hỏi liên quan
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
Chọn đáp án C.
Gọi M(x;y;z) ta có
hệ điều kiện
Đúng 0
Bình luận (0)
Trong không gian tọa độ Oxyz, cho hai điểm
A
(
1
;
0
;
0
)
,
B
(
5
;
0
;
0
)
. Gọi (H) là tập hợp các điểm M trong không gian thỏa mãn
M
A
→
.
M
B
→
0
. Khẳng định nào sau đây là đúng? A. (H) là một đường tròn có bán k...
Đọc tiếp
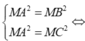
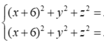
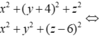
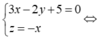
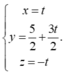
Trong không gian tọa độ Oxyz, cho hai điểm A ( 1 ; 0 ; 0 ) , B ( 5 ; 0 ; 0 ) . Gọi (H) là tập hợp các điểm M trong không gian thỏa mãn M A → . M B → = 0 . Khẳng định nào sau đây là đúng?
A. (H) là một đường tròn có bán kính bằng 4
B. (H) là một mặt cầu có bán kính bằng 4
C. (H) là một đường tròn có bán kính bằng 2
D. (H) là một mặt cầu có bán kính bằng 2
Trong không gian tọa độ Oxyz cho các điểm A(2; 0; 0), A’(6; 0; 0), B(0; 3; 0), B’(0 ;4; 0), C(0; 0; 4), C’(0; 0; 3).
Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
Đúng 1
Bình luận (0)
Tọa độ điểm \(G\) là \(G\left(\dfrac{6+0+0}{3},\dfrac{0+4+0}{3},\dfrac{0+0+3}{3}\right)\) suy ra \(G\left(2,\dfrac{4}{3},1\right)\).
\(\overrightarrow{AB}=\left(-2,3,0\right),\overrightarrow{BC}=\left(0,-3,4\right),\overrightarrow{CA}=\left(2,0,-4\right)\)
Đặt \(H\left(a,b,c\right)\).
Vì \(H\) là trực tâm tam giác \(ABC\) nên
\(\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{CA}=0\\\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AH}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3b+4c=0\\2a-4c=0\\12\left(a-2\right)+8b+6c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{72}{61}\\b=\dfrac{48}{61}\\c=\dfrac{36}{61}\end{matrix}\right.\) suy ra \(H\left(\dfrac{72}{61},\dfrac{48}{61},\dfrac{36}{61}\right)\).
\(\overrightarrow{OG}=\left(2,\dfrac{4}{3},1\right)\)
Đường thẳng qua OG: \(\left\{{}\begin{matrix}x=2t\\y=\dfrac{4}{3}t\\z=t\end{matrix}\right.\).
Bằng cách thử trực tiếp, ta thấy H nằm trên đường thẳng OG.
Đúng 1
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(a;0;0), B(0;b;0), C(0;0;c) với
a
b
c
≠
0
. Phương trình mặt phẳng (ABC) là A.
x
a
+
y
b
+
z
c
+
1
0
B.
x
a
+
y
b
+
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(a;0;0), B(0;b;0), C(0;0;c) với a b c ≠ 0 . Phương trình mặt phẳng (ABC) là
A. x a + y b + z c + 1 = 0
B. x a + y b + z c = 0
C. x a + y b + z c − 1 = 0
D. a x + b y + c z − 1 = 0
Trong không gian Oxyz cho các điểm A(-3;0;0); B(0;-3;0); C(0;0;6) Tính khoảng cách từ điểm M(1;-3;-4) đến mặt phẳng (ABC)
A. 4
B. 2
C. 1
D. 3
Trong không gian Oxyz, viết phương trình tập hợp các điểm M sao cho
A
M
B
^
90
o
với A ( 2;-1;-3 ); B ( 0;-3;5 ) A.
x
-
1
2
+
y
+
2...
Đọc tiếp
Trong không gian Oxyz, viết phương trình tập hợp các điểm M sao cho A M B ^ = 90 o với A ( 2;-1;-3 ); B ( 0;-3;5 )
A. x - 1 2 + y + 2 2 + z - 1 2 = 18
B. x - 1 2 + y - 2 2 + z - 1 2 = 18
C. x - 1 2 + y + 2 2 + z - 1 2 = 3
D. x - 1 2 + y - 2 2 + z - 1 2 = 3
Tập hợp các điểm M là mặt cầu đường kính AB.
Tâm I là trung điểm AB nên I ( 1;-2;1 )
Bán kính: R = IA = 3 2
Vậy phương trình mặt cầu nói trên là
x - 1 2 + y + 2 2 + z - 1 2 = 18
Đáp án A
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai mặt phẳng
α
:2x+y-2z+10;
β
:x-2y+2z+30 Tập hợp tất cả các điểm trong không gian cách đều hai mặt phẳng đã cho là A. Một mặt phẳng duy nhất B. Một điểm duy nhất C. Hai mặt phẳng phân biệt vuông góc với nhau D. Một đường thẳng duy nhất song song với cả hai mặt phẳng đã cho
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng α :2x+y-2z+1=0; β :x-2y+2z+3=0 Tập hợp tất cả các điểm trong không gian cách đều hai mặt phẳng đã cho là
A. Một mặt phẳng duy nhất
B. Một điểm duy nhất
C. Hai mặt phẳng phân biệt vuông góc với nhau
D. Một đường thẳng duy nhất song song với cả hai mặt phẳng đã cho
Điểm cần tìm M(x;y;z) ta có điều kiện cách đều hai mặt phẳng là
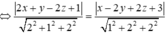
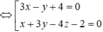
Vậy tập hợp các điểm này nằm trên hai mặt phẳng vuông góc với nhau (hai mặt phẳng này được gọi là mặt phẳng phân giác của góc tạo bởi hai mặt phẳng).
Chọn đáp án C.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ
A
B
→
là A.
A
B
→
1
;
-
1
;
1
B.
A
B
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ A B → là
A. A B → = 1 ; - 1 ; 1
B. A B → = 1 ; 1 ; - 3
C. A B → = 3 ; - 3 ; 3
D. A B → = 3 ; - 3 ; - 3
Trong không gian Oxyz, cho mặt phẳng (P): x-2y+z-5=0. Trong các điểm A(0;0;5), B(1;1;3), C(-1;2;3), D(2;1;5), có bao nhiêu điểm thuộc mặt phẳng (P)?
A. 4.
B. 3.
C. 2.
D. 1.
Trong không gian tọa độ Oxyz cho hình hộp ABCD.A’B’C’D’ với các điểm A(-1;1;2), B(-3;2;1), D(0;-1;2) và A(2;1;2). Tìm tọa độ đỉnh C’
Đọc tiếp
Trong không gian tọa độ Oxyz cho hình hộp ABCD.A’B’C’D’ với các điểm A(-1;1;2), B(-3;2;1), D(0;-1;2) và A(2;1;2). Tìm tọa độ đỉnh C’
