Cho số phức z thỏa mãn z - 3 + 4 i = 4 . Giá trị lớn nhất của z 2 là
A. 44
B. 65
C. 81
D. 100
Những câu hỏi liên quan
Cho z là số phức thay đổi thỏa mãn
(
1
+
i
)
z
+
2
-
i
4
và M(x,y) là điểm biểu diễn cho z trong mặt phẳng phức. Tìm giá trị lớn nhất của biểu thức
T
x
+
y
+...
Đọc tiếp
Cho z là số phức thay đổi thỏa mãn ( 1 + i ) z + 2 - i = 4 và M(x,y) là điểm biểu diễn cho z trong mặt phẳng phức. Tìm giá trị lớn nhất của biểu thức T = x + y + 3
A. T = 4 + 2 2
B. 8
C. 4
D. 4 2
Cho số phức z thỏa mãn |z – 4| + |z + 4| 10. Giá trị lớn nhất và nhỏ nhất của mô – đun của số phức z là A. 10 và 4 B. 5 và 4 C. 4 và 3 D. 5 và 3
Đọc tiếp
Cho số phức z thỏa mãn |z – 4| + |z + 4| = 10. Giá trị lớn nhất và nhỏ nhất của mô – đun của số phức z là
A. 10 và 4
B. 5 và 4
C. 4 và 3
D. 5 và 3
Chọn D.
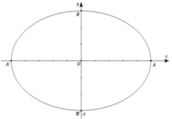
Giả sử z = x + yi có điểm biểu diễn là M(x; y).
Giả sử F1( 4 ; 0) ; F2( 0 ; -4) khi đó tập hợp các điểm M thỏa mãn là MF1+ MF2= 10 là đường elip (E) có các tiêu điểm là F1 ; F2 và trục lớn bằng 10.
Từ đó ta tìm được 2c = F1F2 = 8 nên c = 4.
2a = 10 nên a = 5
suy ra b2 = a2 - c2 = 9 nên b = 3.
Từ đó 
Vì M di động trên (E) nên |z| = OM lớn nhất, nhỏ nhất khi OM lần lượt là độ dài nửa bán trục lớn, nửa bán trục nhỏ. Hay max |z| = 5 ; min |z| = 3.
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn z - 4 + z + 4 = 10 . Giá trị lớn nhất và giá trị nhỏ nhất của z lần lượt là:
A. 10 và 4
B. 5 và 4
C. 4 và 3
D. 5 và 3
Cho số phức z thỏa mãn |z-4|+|z+4|=10. Giá trị lớn nhất và giá trị nhỏ nhất của |z| lần lượt là:
A. 10 và 4
B. 5 và 4
C. 4 và 3
D. 5 và 3
Cho số phức
z
a
+
b
i
thỏa mãn
z
-
i
2
v
à
z
+
3
i
+
2
z
-
4
-
i
đạt giá trị nhỏ nhất. Tổng...
Đọc tiếp
Cho số phức z = a + b i thỏa mãn z - i = 2 v à z + 3 i + 2 z - 4 - i đạt giá trị nhỏ nhất. Tổng a + b bằng
A. 3 + 6 13 17
B. 1 + 2 13 17
C. 5 + 10 13 17
D. 5 - 10 13 17
Chọn C
Cách giải:
=>M thuộc đường tròn (C) tâm I(0,1), R=2
Mà M nằm trên (C) => M là giao điểm của (C) và OB
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
-
1
z
+
3
i
1
2
.
Tìm giá trị lớn nhất của biểu thức
P
z
+
i
+
2
z...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 z + 3 i = 1 2 . Tìm giá trị lớn nhất của biểu thức P = z + i + 2 z ¯ - 4 + 7 i
A. 10
B. 20
C. 2 5
D. 4 5
Cho số phức z thỏa mãn
z
−
1
z
+
3
i
1
2
.
Tìm giá trị lớn nhất của biểu thức
P
z
+
i
+
2
z...
Đọc tiếp
Cho số phức z thỏa mãn z − 1 z + 3 i = 1 2 .
Tìm giá trị lớn nhất của biểu thức P = z + i + 2 z ¯ − 4 + 7 i
A. 8
B. 10
C. 2 5
D. 4 5
Đáp án B
Đặt z = x + y i x , y ∈ ℝ , khi đó z − 1 z + 3 i = 1 2 ⇔ 2 z − 1 = z + 3 i
⇔ 2 x − 1 2 + y 2 = x 2 + y + 3 2 ⇔ x − 2 2 + y − 3 2 = 20 C
Suy ra tập hợp điểm biểu diễn số phức z là đường tròn (C), tâm I 2 ; 3 , bán kính R = 2 5
Ta có P = z + i + 2 z ¯ − 4 + 7 i = z + i + 2 z − 4 + 7 i , với A 0 ; − 1 , B 4 ; 7 ⇒ P = M A + 2 M B
Vậy P = M A + 2 M B ≤ 1 2 + 2 2 M A 2 + M B 2 = 5.20 = 10 → P m a x = 10
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
-
1
z
+
3
i
1
2
. Tìm giá trị lớn nhất của biểu thức
P
z
+...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 z + 3 i = 1 2 .
Tìm giá trị lớn nhất của biểu thức P = z + i + 2 z ¯ - 4 + 7 i .
A. 10
B. 20
C. 2 5
D. 4 5
Đáp án B
Ta có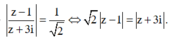 
Gọi M là điểm biểu diễn số phức, tập hợp điểm biểu diễn số phức z là đường tròn có phương trình
A(0;-1), B(4;7) lần lượt biểu diễn 2 số phức 
Ta có 
nên AB là bán kính đường tròn (C)
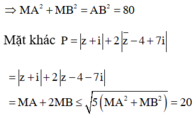
Dấu “=” xảy ra khi MB=2MA
Vậy maxP= 20
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
-
1
z
+
3
i
1
2
. Tìm giá trị lớn nhất của biểu thức
P
z
+
i
+
2
z...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 z + 3 i = 1 2 . Tìm giá trị lớn nhất của biểu thức P = z + i + 2 z - 4 + 7 i
A. 8
B. 10
C. 2 5
D. 4 5
