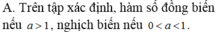
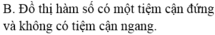
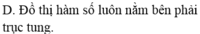
Khẳng định nào dưới đây là sai khi nói về hàm số y = log a x (với 0 < a ≠ 1 ) ?
A. Trên tập xác định, hàm số đồng biến nếu a > 1, nghịch biến nếu 0 < a < 1.
B. Đồ thị hàm số có một tiệm cận đứng và không có tiệm cận ngang.
C. Tập xác định của hàm số là ℝ .
D. Đồ thị hàm số luôn nằm bên phải trục tung.
Chọn C
+ Hàm số y = log a x (với 0 < a ≠ 1 ) có tập xác định là D = ( 0 ; + ∞ ) . Do đó đáp án C sai.
Khẳng định nào dưới đây là sai khi nói về hàm số y = log a x ( v ớ i 0 < a ≠ 1 ) (với ) ?
A. Trên tập xác định, hàm số đồng biến nếu a > 1, nghịch biến nếu 0<a<1
B. Đồ thị hàm số có một tiệm cận đứng và không có tiệm cận ngang
C. Tập xác định của hàm số là R
D. Đồ thị hàm số luôn nằm bên phải trục tung
Cho hàm số f x = x 2 + x k h i x ≥ 0 x k h i x < 0 . Khẳng định nào dưới đây là sai?
A. f’(0+) = 1.
B. f’(0-) = 1.
C. df(0) = dx.
D. Hàm số không có vi phân tại x = 0.
Cho bốn số thực dương a, b, x, y với \(a,b \ne 1\). Khẳng định nào sau đây là sai?
A. \({\log _a}(xy) = {\log _a}x + {\log _b}y\).
B. \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
C. \({\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\).
D. \({\log _a}b \cdot {\log _b}x = {\log _a}x\).
Bảng biến thiên dưới đây là của hàm số nào
Cho 0<a khác 1, b>0, c>0. Hỏi khẳng định nào dưới đây là sai
A. log a b c = log a b + log a c
B. log a b c = log a b - log a c
C. a log b c = c log b a
D. a log a b = a
Cho hàm số y = f ( x ) = a x 4 + b 2 x 2 + 1 ( a ≢ 0 ) Trong các khẳng định dưới đây, khẳng định nào là đúng?
A. Hàm số nhận gốc tọa độ làm tâm đối xứng.
B. Hàm số nhận trục hoành làm trục đối xứng.
C. Với a > 0, hàm số có ba điểm cực trị luôn tạo thành một tam giác cân.
D. Với mọi giá trị của tham số a , b ( a ≢ 0 ) thì hàm số luôn có cực trị.
Cho hai số dương a và b. Đặt X = log a + b 2 , Y = log a + log b 2 . Khẳng định nào dưới đây là đúng
Cho hàm số f x = 3 - x 2 2 k h i x < 1 1 x k h i x ≥ 1 . Khẳng định nào dưới đây là sai?
A. Hàm số f(x) liên tục tại x = 1
B. Hàm số f(x) có đạo hàm tại x = 1
C. Hàm số f(x) liên tục và có đạo hàm tại x = 1
D. Hàm số f(x) không có đạo hàm tại x = 1
Cho hàm số f x = 3 − x 2 2 k h i x < 1 1 x k h i x < 1 . Khẳng định nào dưới đây là sai?
A. Hàm số f(x) liên tục tại x = 1
B. Hàm số f(x) có đạo hàm tại x = 1
C. Hàm số f(x) liên tục tại x = 1 và hàm số f(x) cũng có đạo hàm tại x = 1
D. Hàm số f(x) không có đạo hàm tại x = 1
Đáp án C.
Ta có
f 1 = lim x → 1 + f 1 = 1 lim x → 1 − f 1 = lim x → 1 + 3 − x 2 2 = 1 ⇒ f 1 = lim x → 1 + f 1 = lim x → 1 − f 1 .
Hàm số liên tục tại x = 1
Xét
lim x → 1 − f x − f 1 x − 1 = lim x → 1 − 3 − x 2 2 − 1 x − 1 = lim x → 1 − − 1 − x 2 = − 1 lim x → 1 + = f x − f 1 x − 1 = lim x → 1 − 1 x − 1 x − 1 = lim x → 1 − − x = − 1 .
Hàm số có đạo hàm tại x = 1
