Các câu hỏi tương tự
Cho hàm số
f
(
x
)
x
2
sin
1
x
n
ế
u
x
...
Đọc tiếp
Cho hàm số f ( x ) = x 2 sin 1 x n ế u x ≠ 0 A n ế u x = 0
Xác định A để f(x) liên tục tại x = 0. Với giá trị A tìm được, hàm số có đạo hàm tại x = 0 không?
Cho hàm số
f
(
x
)
2
x
+
8
-
2
x
+
2
...
Đọc tiếp
Cho hàm số f ( x ) = 2 x + 8 - 2 x + 2 K h i x > - 2 0 x = - 2 . Tìm khẳng định đúng trong các khẳng định sau:
(I) lim x → 2 + f ( x ) = 0 .
(II) f(x) liên tục tại x = -2
(III) f(x) gián đoạn tại x= -2
A. Chỉ (I) và (III).
B. Chỉ (I) và (II).
C. Chỉ (I).
D. Chỉ (II)
Cho hàm số
f
(
x
)
2
x
+
8
-
2
x
+
2
...
Đọc tiếp
Cho hàm số f ( x ) = 2 x + 8 - 2 x + 2 x > - 2 0 x = - 2 Tìm khẳng định đúng trong các khẳng định sau:
(I) lim x → - 2 + f ( x ) = 0
(II) f(x) liên tục tại x = -2
(III) f(x)gián đoạn tại x = -2
A. Chỉ (I) và (III).
B. Chỉ (I) và (II).
C. Chỉ (I).
D. Chỉ (II).
Cho hàm số
f
(
x
)
x
+
1
+
x
-
1
3
x
...
Đọc tiếp
Cho hàm số f ( x ) = x + 1 + x - 1 3 x k h i x k h á c 0 2 k h i x = 0 Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x = 0
B. Hàm số liên tục tại mọi điểm như gián đoạn tại x = 0
C. Hàm số không liên tục tại x = 0
D. Tất cả đều sai
Cho a,b,c,d là các số thực khác 0 và hàm số yf(x) asincx + bcosdx. Khẳng định nào sau đây là đúng? A. yf(x) asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi
c
d
là số hữu tỉ. B. yf(x) asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi
a
d
là số hữu tỉ. C. yf(x) asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi
c
b...
Đọc tiếp
Cho a,b,c,d là các số thực khác 0 và hàm số
y=f(x)= asincx + bcosdx. Khẳng định nào sau đây là đúng?
A. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi c d là số hữu tỉ.
B. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi a d là số hữu tỉ.
C. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi c b là số hữu tỉ.
D. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi a x là số hữu tỉ.
Cho hàm số
f
x
2
x
+
8
-
2
x
+
2
x
-
2...
Đọc tiếp
Cho hàm số f x = 2 x + 8 - 2 x + 2 x > - 2 0 x = - 2 . Tìm khẳng định đúng trong các khẳng định sau:
(I) lim x → 2 + f x = 0
(II) f(x) liên tục tại x = -2
(III) f(x) gián đoạn tại x = -2
A. Chỉ (I) và (III).
B. Chỉ (I) và (II) .
C. Chỉ (I) .
D. Chỉ (II) .
Cho hàm số f(x) xác định bởi
f
(
x
)
x
2
+
1
-
x
x
(
x...
Đọc tiếp
Cho hàm số f(x) xác định bởi f ( x ) = x 2 + 1 - x x ( x ≠ 0 ) 0 ( x = 0 ) . Giá trị f’(0) bằng:
A. 0
B. 1
C. 1/2.
D. Không tồn tại.
Cho hàm số
f
(
x
)
3
-
4
-
x
4
k
h
i
x...
Đọc tiếp
Cho hàm số f ( x ) = 3 - 4 - x 4 k h i x ≢ 0 1 4 k h i x = 0 . Khi đó đạo hàm của hàm số tại điểm x = 0 là kết quả nào sau đây?
A. 1 4
B. 1 16
C. 1 32
D. Không tồn tại
Cho hàm số
f
(
x
)
tan
x
x
;
x
k
h
á...
Đọc tiếp
Cho hàm số f ( x ) = tan x x ; x k h á c 0 ∧ x k h á c π 2 + k π ; k ∈ ℤ 0 ; x = 0 Hàm số y = f(x) liên tục trên các khoảng nào sau đây?
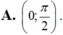
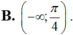
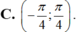
![]()



