Parabol y = x 2 2 chia hình tròn có tâm là gốc tọa độ, bán kính bằng 2 2 thành hai phần có diện tích là S 1 và S 2 , trong đó S 1 < S 2 . Tìm tỉ số S 1 S 2
A. 3 π + 2 21 π - 2
B. 3 π + 2 9 π - 2
C. 3 π + 2 12 π
D. 9 π - 2 3 π + 2
Những câu hỏi liên quan
Parabol \(y=\dfrac{x^2}{2}\) chia hình tròn có tâm tại gốc tọa độ, bán kính \(2\sqrt{2}\) thành hai phần. Tìm tỉ số diện tích của chúng ?
Parabol
y
x
2
2
chia hình tròn có tâm là gốc tọa độ, bán kính bằng
2
2
thành hai phần có diện tích
S
1
và
S
2
, trong đó
S
1
S
2
. Tìm tỉ số
S...
Đọc tiếp
Parabol y = x 2 2 chia hình tròn có tâm là gốc tọa độ, bán kính bằng 2 2 thành hai phần có diện tích S 1 và S 2 , trong đó S 1 < S 2 . Tìm tỉ số S 1 S 2
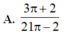
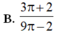
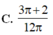
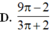
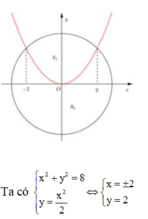
Ta có parabol và đường tròn như hình vẽ bên
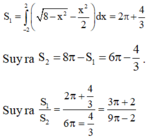
Đáp án B
Đúng 0
Bình luận (0)
Parabol y = x 2 2 chia hai đường tròn có tâm tại gốc tọa độ, bán kính bằng 2 2 thành 2 phần. Tỉ số diện tích của chúng thuộc khoảng nào trong các khoảng sau đây?
A. (0,4;0,5)
B. (0,5;0,6)
C. (0,6;0,7)
D. (0,7;0,8)
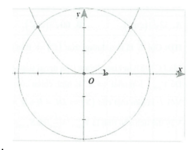
Diện tích phần giới hạn giữa đường tròn và parabol là:
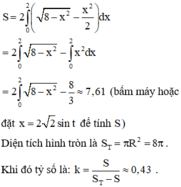
Chọn A.
Đúng 0
Bình luận (0)
Gọi S là diện tích của hình phẳng giới hạn bởi parabol
y
x
2
2
và đường tròn có tâm tại gốc tọa độ, bán kính bằng
2
2
. Biết
S
a
π
+
b
c
, trong đó
a
,
b
,
c
∈
ℕ
*
,
b...
Đọc tiếp
Gọi S là diện tích của hình phẳng giới hạn bởi parabol y = x 2 2 và đường tròn có tâm tại gốc tọa độ, bán kính bằng 2 2 . Biết S = a π + b c , trong đó a , b , c ∈ ℕ * , b , c = 1 . Tính tổng a + b + c .
A. 6
B. 7
C. 8
D. 9
Gọi S là diện tích của hình phẳng giới hạn bởi parabol
y
x
2
2
và đường tròn có tâm tại gốc tọa độ, bán kính bằng
2
2
. Biết
S
a
π
+
b
c
, trong đó
a
,
b
,
c
∈
ℕ
*
,
(
b
,
c
)
1
. Tính tổng
a
+...
Đọc tiếp
Gọi S là diện tích của hình phẳng giới hạn bởi parabol y = x 2 2 và đường tròn có tâm tại gốc tọa độ, bán kính bằng 2 2 . Biết S = a π + b c , trong đó a , b , c ∈ ℕ * , ( b , c ) = 1 . Tính tổng a + b + c .
A. 6
B. 7
C. 8
D. 9
Đáp án D.
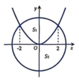
Phương trình đường tròn tâm O có bán kính R = 2 2 là x 2 + y 2 = 8 .
Ta có parabol và đường tròn như hình vẽ bên.
Giao điểm của parabol và đường tròn là nghiệm của hệ phương trình
x 2 + y 2 = 8 y = x 2 2 ⇔ x = ± 2 y = 2
Vì parabol và đường tròn đều đối xứng qua trục Oy nên ta có
S = 2 ∫ 0 2 8 - x 2 - x 2 2 d x .
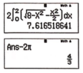
Bấm máy tính, ta được kết quả như hình bên. Ta biết S = a π + b c nên ta thao tác tiếp theo trên máy như hình bên.
Vậy ta có S = 2 π + 4 3 . Do đó ta có a = 2 , b = 4 , c = 3 ⇒ a + b + c = 9 . Chọn đáp án D.
Đúng 0
Bình luận (0)
Đường tròn x^2+y^2-4x-6y=12 có tâm I và bán kính R. Với O là gốc tọa độ, mệnh đề nào đúng?
A.OI>R
B. OI=R
C.5OI=R4,123
D.5OI=R3,742
Pt đường tròn đã cho có thể viết dưới dạng:
\(\left(x-2\right)^2+\left(y-3\right)^2=25\)
Ta tìm được tọa độ tâm I là \(I\left(2;3\right)\). Do đó \(OI=\sqrt{2^2+3^2}=\sqrt{13}\).
Đồng thời \(R=5\)
Ta có \(\dfrac{OI}{R}=\dfrac{\sqrt{13}}{5}\Leftrightarrow5OI=R\sqrt{13}\approx R.3,606\)
(Bạn xem lại đề nhé, với kết quả này thì mình không thấy mệnh đề nào trong 4 mệnh đề kia đúng cả.)
Đúng 1
Bình luận (0)
cho đường tròn có tâm là gốc tọa độ bán kính 2√2 và đường thẳng (d):y+m^2+2=x.với m<0 để đường thẳng (d) tiếp xúc với đường tròn thì m bẳng bao nhiêu
M(x,y) thuộc đường tròn có tâm là gốc tọa độ 0 và bán kính là căn 5 khi nào nhỉ?
cho đường tròn có tâm là gốc tọa độ bán kính \(2\sqrt{2}\) và đường thẳng \(\left(d\right):y+m^2+2=x\).với m<0 để đường thẳng (d) tiếp xúc với đường tròn thì m bẳng bao nhiêu