Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, S A ⊥ ( A B C D ) . Biết SA=y, M ∈ A D , AM=x, x 2 + y 2 = a 2 . Khi đó giá trị lớn nhất của V S . A B C M là:
A. a 3 3 4
B. a 3 8
C. a 3 3 2
D. a 3 3 8
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,
S
A
⊥
(
A
B
C
D
)
. Biết
S
A
y
;
M
∈
A
D
;
A...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, S A ⊥ ( A B C D ) . Biết S A = y ; M ∈ A D ; A M = x ; x 2 + y 2 = a 2 . Khi đó giá trị lớn nhất của V S . A B C M là:
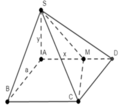
A. a 3 3 4
B. a 3 8
C. a 3 3 2
D. a 3 3 8
Đáp án D
Ta có: S A B C M = A M + B C 2 . A B = a ( x + a ) 2 (đvdt)
⇒ V S . A B C M = 1 3 . S A . S A B C M = a ( x + a ) a 2 - x 2 6 (đvtt).
Đặt f ( x ) = ( x + a ) a 2 - x 2
Xét phương trình f ' ( x ) = 0 ⇒ x = a 2
⇒ f ( x ) đạt giá trị lớn nhất khi x = a 2
Từ đó suy ra V S . A B C M m a x = a 3 3 8 (đvtt).
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Gọi E là trung điểm BC, góc giữa SC và mặt phẳng (SAB) bằng
30
o
.
Khoảng cách giữa DE và SC là A.
a
38
19
B.
a
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Gọi E là trung điểm BC, góc giữa SC và mặt phẳng (SAB) bằng 30 o . Khoảng cách giữa DE và SC là
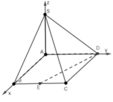
A. a 38 19
B. a 2 7
C. 2 a 9
D. 2 a 3 9
Đáp án A
Xét ∆ S B C vuông tại B,nên dễ tính được S B = a 3
Từ đó suy ra S A = a 2
Gắn trục tọa độ Axyz với A là gốc tọa độ sao cho:
Tia Ax trùng tia AB; tia Ay trùng tia AD; tia Az trùng tia AS.
Khi đó:
Phương trình mặt phẳng qua DE và song song với SC là:
Do đó, khoảng cách giữa hai đường thẳng ED và SC là:
d ( E D ; S C ) = d ( S ; ( P ) ) = a 38 19
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Gọi E là trung điểm BC, góc giữa SC và mặt phẳng (SAB) bằng
30
°
. Khoảng cách giữa DE và SC là A.
a
38
19
B.
a
2
7
C.
2
a
9
D. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Gọi E là trung điểm BC, góc giữa SC và mặt phẳng (SAB) bằng 30 ° . Khoảng cách giữa DE và SC là
A. a 38 19
B. a 2 7
C. 2 a 9
D. 2 a 3 9
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng đáy là I thuộc AB sao cho BI2AI. Góc giữa mặt bên (SCD) và mặt đáy bằng
60
°
. Khoảng cách giữa AD và SC là: A.
3
a
93
31
B.
4
a
93
31
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng đáy là I thuộc AB sao cho BI=2AI. Góc giữa mặt bên (SCD) và mặt đáy bằng 60 ° . Khoảng cách giữa AD và SC là:
A. 3 a 93 31
B. 4 a 93 31
C. 5 a 93 31
D. 6 a 93 31
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng đáy là I thuộc AB sao cho BI 2AI. Góc giữa mặt bên (SCD) và mặt đáy bằng
60
o
Khoảng cách giữa AD và SC là: A.
3
a
93
31
B.
4...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng đáy là I thuộc AB sao cho BI = 2AI. Góc giữa mặt bên (SCD) và mặt đáy bằng 60 o Khoảng cách giữa AD và SC là:
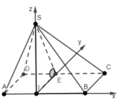
A. 3 a 93 31
B. 4 a 93 31
C. 5 a 93 31
D. 6 a 93 31
Cho hı̀nh chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), đáy là hình thang ABCD vuông tại A và B có ABa, AD3a, BCa. Biết SAa
3
. Tính thể tích khối chóp S.BCD theo a.
Đọc tiếp
Cho hı̀nh chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), đáy là hình thang ABCD vuông tại A và B có AB=a, AD=3a, BC=a. Biết SA=a 3 . Tính thể tích khối chóp S.BCD theo a.
Cho hı̀nh chóp S.ABCD có SA vuông góc với mặt phẳng
A
B
C
D
, đáy là hình thang ABCD vuông tại A và B có
A
B
a
,
A
D
3
a
,
B
C
a
. Biết
S
A
a
3
, tính thể tích khối chóp S.BCD theo...
Đọc tiếp
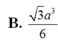
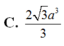
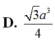
Cho hı̀nh chóp S.ABCD có SA vuông góc với mặt phẳng A B C D , đáy là hình thang ABCD vuông tại A và B có A B = a , A D = 3 a , B C = a . Biết S A = a 3 , tính thể tích khối chóp S.BCD theo a
A. 2 3 a 3
B. 3 a 3 6
C. 2 3 a 3 3
D. 3 a 3 4
Đáp án B
V S . B C D = 1 3 S A . S Δ B C D = 1 3 . S A . 1 2 . A B . B C = 1 3 . a 3 . 1 2 . a . a = a 3 3 6 .
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB BC a, AD 2a. Cạnh SA2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và
α
là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng với hình chóp S.ABCD là A.
S
a
2
B.
S
3
a
2...
Đọc tiếp
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh SA=2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và α là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng với hình chóp S.ABCD là
A. S = a 2
B. S = 3 a 2 2
C. S = a 2 2
D. S = 2 a 2
Đáp án A.
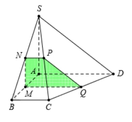
Gọi N, Q lần lượt là trung điểm của AB, CD ⇒ M N ⊥ A B M Q ⊥ A B .
Qua N kẻ đường thẳng song song với BC, cắt SC tại P.
Suy ra thiết diện của mặt phẳng α và hình chóp là MNPQ.
Vì MQ là đường trung bình của hình tháng ABCD ⇒ M Q = 3 a 2 .
MN là đường trung bình của tam giác SAB ⇒ M N = S A 2 = a .
NP là đường trung bình của tam giác SBC ⇒ N P = B C 2 = a 2 .
Vậy diện tích hình thang MNPQ là S M N P Q = M N . N P + M Q 2 = a 2 a 2 + 3 a 2 = a 2 .
Đúng 1
Bình luận (0)
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với ABBCa ,AD2a Cạnh SA2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và
(
α
)
là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng
(
α
)
với hình chóp S.ABCD là
Đọc tiếp
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB=BC=a ,AD=2a Cạnh SA=2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và ( α ) là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng ( α ) với hình chóp S.ABCD là
