Cho khối hộpABCD.A'B'C'D' có thể tích V . Các điểm M , N , P thỏa mãn A M → = 2 A C → , A N → = 3 A B ' → , A P → = 4 A D ' → . Tính thể tích khối chóp AMNP theo V .
A. 6V.
B. 8V.
C. 12V.
D. 4V.
Những câu hỏi liên quan
Cho khối hộpABCD,ABCD có thể tích V . Các điểm M , N , P thỏa mãn
A
M
→
2
A
C
,
→
A
N
→
3
A
B
→
,
A...
Đọc tiếp
Cho khối hộpABCD,A'B'C'D' có thể tích V . Các điểm M , N , P thỏa mãn A M → = 2 A C , → A N → = 3 A B ' → , A P → = 4 A D ' → . Tính thể tích khối chóp AMNP theo V
A. 6V
B. 8V.
C. 12V
D. 4V.
Cho hình chóp S.ABC có thể tích V. Gọi M, N, P là các điểm thỏa mãn
S
A
2
S
M
;
S
B
2
S
N
;
S
C
1
2
S
P
Tính thể tích của khối chóp S.MNP theo V. A.
V
3
B.
V
4
C.
V
2...
Đọc tiếp
Cho hình chóp S.ABC có thể tích V. Gọi M, N, P là các điểm thỏa mãn S A = 2 S M ; S B = 2 S N ; S C = 1 2 S P Tính thể tích của khối chóp S.MNP theo V.
A. V 3
B. V 4
C. V 2
D. V 5
Đáp án C
Ta có
V S . A B C V S M N P = S A S M . S B S N . S C S P = 2 S M S M . 2 S N S N . 1 2 S P S P = 2
⇒ V S M N P = 1 2 V S A B C = V 2
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có thể tích V. Gọi M, N, P là các điểm thỏa mãn SA 2SM; SB 2SN; SC
1
2
SP. Tính thể tích của khối chóp S.MNP theo V.
A
.
V
3
B
.
V
4
C
.
V
2
D
.
V
5
Đọc tiếp
Cho hình chóp S.ABC có thể tích V. Gọi M, N, P là các điểm thỏa mãn SA = 2SM; SB = 2SN; SC = 1 2 SP. Tính thể tích của khối chóp S.MNP theo V.
A . V 3
B . V 4
C . V 2
D . V 5
Cho khối hộpABCD.ABCD Gọi M là trung điểm của cạnh AB. Mặt phẳng (MBD) chia khối hộp thành hai phần. Tính tỉ số thể tích hai phần đó. A.
5
12
B.
7
17
C.
7
24
D.
5
17
Đọc tiếp
Cho khối hộpABCD.A'B'C'D' Gọi M là trung điểm của cạnh AB. Mặt phẳng (MB'D') chia khối hộp thành hai phần. Tính tỉ số thể tích hai phần đó.
A. 5 12
B. 7 17
C. 7 24
D. 5 17
Đáp án B
Dựng MN//BD//B'D'
Chia thể tích khối A'B'D'.AMN thành 3 khối chóp
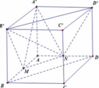
Ta có: V A ' B ' D ' . A M N = V N . A ' B ' D ' + V N . A ' B ' M ' + V A ' . A M N
= 1 2 V N . A ' B ' C ' D ' + 1 2 V D . A ' B ' M + 1 4 V A ' . A B D
= 1 6 V + 1 2 V D ' . A ' B ' M + 1 24 V = 1 6 V + 1 12 V + 1 24 V = 7 24 V
Do đó tỷ số thể tích 2 phần là V 1 V 2 = 7 17
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn
S
M
1
4
S
A
,
S
N
1
3
S
B
,
S
P
3
S
C
Thể tích của khối chóp S.MNP theo V A.
V
5
B.
V
4
C.
V
3
D. ...
Đọc tiếp
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn S M = 1 4 S A , S N = 1 3 S B , S P = 3 S C Thể tích của khối chóp S.MNP theo V
A. V 5
B. V 4
C. V 3
D. V 2
Cho hình hộp ABCD.A’B’C’D’ có thể tích V, gọi M, N là hai điểm thỏa mãn
D
M
→
2
M
D
→
,
C
N
→
2
N
C
→
, đường thẳng AM cắt đường thẳng A’D’ tại P, đ...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có thể tích V, gọi M, N là hai điểm thỏa mãn D ' M → = 2 M D → , C ' N → = 2 N C → , đường thẳng AM cắt đường thẳng A’D’ tại P, đường thẳng BN cắt đường thẳng B’C’ tại Q. Thể tích của khối PQNMD’C’ bằng
A. 2 3 V
B. 1 3 V
C. 1 2 V
D. 3 4 V
Cho hình hộp ABCD.ABCD có thể tích V, gọi M, N là hai điểm thỏa mãn
D
M
→
2
M
D
→
,
C
N
→
2
N
C
→
, đường thẳng AM cắt đường thẳng AD tại P, đường t...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có thể tích V, gọi M, N là hai điểm thỏa mãn D ' M → = 2 M D → , C ' N → = 2 N C → , đường thẳng AM cắt đường thẳng A'D' tại P, đường thẳng BN cắt đường thẳng B'C' tại Q. Thể tích của khối PQNMD'C' bằng
Cho lăng trụ ABC.A’B’C’ có thể tích bằng 72. Gọi M là trung điểm cạnh A’B’; các điểm N, P thỏa mãn
B
N
⇀
3
4
B
C
⇀
;
B
P
⇀
1
4...
Đọc tiếp
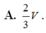
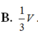
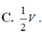
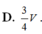
Cho lăng trụ ABC.A’B’C’ có thể tích bằng 72. Gọi M là trung điểm cạnh A’B’; các điểm N, P thỏa mãn B ' N ⇀ = 3 4 B ' C ' ⇀ ; B P ⇀ = 1 4 B C ⇀ Đường thẳng NP cắt BB’ tại E; đường thẳng ME cắt AB tại Q. Thể tích khối đa diện ACPQA'C'NM bằng
A. 55
B. 59
C. 52
D. 56
Thể tích khối lăng trụ đã cho là V 0 = S h = 72 Ta có
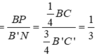
Do đó
Vì vậy khối chóp cụt BQP.B′MN có thể tích là
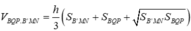
Do đó 
=72-13=59
Chọn đáp án B.
Cách 2: Dùng tỉ số thể tích có:
Vì vậy 
=72-13=59
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho khối hộpABCD.A'B'C'D có thể tích bằng 9. Tính thể tích khối tứ diện ACB'D'.
A. 3
B. 9 2
C. 6
D. 27 4
