Thể tích khối lăng trụ đã cho là V 0 = S h = 72 Ta có

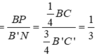

Do đó


Vì vậy khối chóp cụt BQP.B′MN có thể tích là
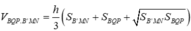

![]()
Do đó ![]()

=72-13=59
Chọn đáp án B.
Cách 2: Dùng tỉ số thể tích có:

![]()

![]()
![]()

Vì vậy ![]() =72-13=59
=72-13=59
Chọn đáp án B.
Thể tích khối lăng trụ đã cho là V 0 = S h = 72 Ta có

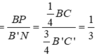

Do đó


Vì vậy khối chóp cụt BQP.B′MN có thể tích là
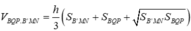

![]()
Do đó ![]()

=72-13=59
Chọn đáp án B.
Cách 2: Dùng tỉ số thể tích có:

![]()

![]()
![]()

Vì vậy ![]() =72-13=59
=72-13=59
Chọn đáp án B.
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AA¢ và BB¢. Đường thẳng CM cắt đường thẳng C’A¢ tại P, đường thẳng CN cắt đường thẳng C‘B¢ tại Q. Thể tích của khối đa diện lồi A’MPB’NQ bằng
A. 1
B. 1 3
C. 1 2
D. 2 3
Cho khối lăng trụ ABC.A'B'C' có thể tích bằng 1. Gọi M, N lần lượt là trung điểm các đoạn thẳng AA' và BB' Đường thẳng CM cắt đường thẳng C'A' tại P, đường thẳng CN cắt đường thẳng C'B' tại Q. Thể tích của khối đa diện lồi A'.MPB'NQ bằng
A. 1
B. 1 3
C. 1 2
D. 2 3
Cho lăng trụ A B C . A ' B ' C ' có thể tích bằng 2. Gọi M, N lần lượt là hai điểm nằm trên cạnh A A ' , B B ' sao cho M là trung điểm của A A ' và B N = 1 2 N B ' . Đường thẳng CM cắt đường thẳng C ' A ' tại P, đường thẳng CN cắt đường thẳng C ' B ' tại Q. Tính thể tích V của khối đa diện A ' M P B ' N Q .
A. V = 13 18
B. V = 23 9
C. V = 5 9
D. V = 7 18
Cho hình lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng 1. Gọi E, F lần lượt là trung điểm AA' và BB' , đường thẳng CE cắt đường thẳng C'A' tại E', đường thẳng CF cắt đường thẳng C'B' tại F'. Thể tích khối đa diện EFB'A'E'F bằng
A. 3 6
B. 3 2
C. 3 3
D. 3 12
Cho hình lăng trụ đều A B C . A ' B ' C ' có tất cả các cạnh bằng 1. Gọi E, F lần lượt là trung điểm của AA’ và BB’; đường thẳng CE cắt đường thẳng C’A’ tại E’, đường thẳng CF cắt đường thẳng C’B’ tại F’. Thể tích khối đa diện E F A ’ B ’ E ’ F ’ bằng
A. 3 12
B. 3 2
C. 3 3
D. 3 6
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = 4, BC = 6 và AA’ = 10. Gọi K, M, N lần lượt là trung điểm của các cạnh BB’, A’B’, BC. Thể tích khối tứ diện C’KMN là:
A. 15
B. 45
C. 5
D. 10
Cho khối lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a.Gọi M, N lần lượt là trung điểm của AB, B′C′. Mặt phẳng (A′MN) cắt cạnh BC tại P. Thể tích của khối đa diện MBP.A′B′N bằng
A. 7 a 3 3 32
B. a 3 3 32
C. 7 a 3 3 68
D. 7 a 3 3 96
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông tại B, AB=a, BC=2a. Hình chiếu vuông góc của A’ trên đáy ABC là trung điểm H của cạnh AC, đường thẳng A’B tạo với đáy một góc 45 ° . Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = a 3 5 6
B. V = a 3 5 3
C. V = a 3 5 2
D. V = a 3 5
Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A’C’, BB’. Thể tích của khối tứ diện CMNP bằng
A. 5 24 V
B. 1 4 V
C. 7 24 V
D. 1 3 V