Cho hai số phức z = 2 x + 3 + 3 y − 1 i và z ' = y − 1 i . Ta có z = z' khi:
A. x = 3 2 ; y = 0
B. x = − 3 2 ; y = 0
C. x = 3 ; y = 1 3
D. x = 0 ; y = − 3 2
Những câu hỏi liên quan
Cho hai số phức z1=1+i , z2=3-7i. Tình modun của số phức z1-z2
\(z_1-z_2=1+i-\left(3-7i\right)=1+i-3+7i=-2+8i\)
\(\Rightarrow\left|z_1+z_2\right|=\sqrt{\left(-2\right)^2+8^2}=2\sqrt{17}\)
Đúng 0
Bình luận (0)
Cho hai số phức
z
1
3
−
7
i
và
z
2
2
+
3
i
. Tìm số phức
z
z
1
+
z
2
. A.
z
1
−
10
i
B.
z
5
−...
Đọc tiếp
Cho hai số phức z 1 = 3 − 7 i và z 2 = 2 + 3 i . Tìm số phức z = z 1 + z 2 .
A. z = 1 − 10 i
B. z = 5 − 4 i
C. z = 3 − 10 i
D. z = 3 + 3 i
Cho hai số phức
z
1
3
-
7
i
và
z
2
2
+
3
i
. Tìm số phức
z
z
1
+
z
2
.
Đọc tiếp
Cho hai số phức z 1 = 3 - 7 i và z 2 = 2 + 3 i . Tìm số phức z = z 1 + z 2 .
Cho hai số phức
z
1
2
+
i
và
z
2
5
-
3
i
. Số phức liên hợp của số phức
z
z
1
(
3
-
2
i
)
+
z
2
là A.
z
¯
-...
Đọc tiếp
Cho hai số phức z 1 = 2 + i và z 2 = 5 - 3 i . Số phức liên hợp của số phức z = z 1 ( 3 - 2 i ) + z 2 là
A. z ¯ = - 13 - 4 i
B. z ¯ = - 13 + 4 i
C. z ¯ = 13 - 4 i
D. z ¯ = 13 + 4 i
Cho số phức z thoả mãn đồng thời hai điều kiện
z
-
3
-
4
i
5
và biểu thức
M
z
+
2
2
-
z
-
i
2
đ...
Đọc tiếp
Cho số phức z thoả mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Môđun của số phức z - 2 - i bằng
A. 5
B. 9
C. 25
D. 5
Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z1; z2 số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?
A. 8i
B. 4
C. -8
D. 8
Chọn D.
Ta có 
+ Giá trị lớn nhất của |z| là 
đạt được tại
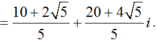
+ Giá trị nhỏ nhất của |z| là 
, đạt được tại
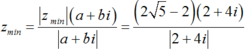
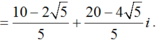
Vậy tổng phần ảo là: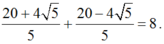 
Đúng 0
Bình luận (0)
Cho hai số phức
z
1
1
+
2
i
;
z
2
3
-
i
Tìm số phức
z
z
2
z
1
A.
z
1
10
+
7
10
i...
Đọc tiếp
Cho hai số phức z 1 = 1 + 2 i ; z 2 = 3 - i Tìm số phức z = z 2 z 1
A. z = 1 10 + 7 10 i
B. z = 1 5 + 7 5 i
C. z = 1 5 - 7 5 i
D. z = - 1 10 + 7 10 i
Cho hai số phức
z
1
1
+
2
i
,
z
2
3
−
i
.
Tìm số phức
z
z
2
z
1
A.
z
1
10
+
7
10
i...
Đọc tiếp
Cho hai số phức z 1 = 1 + 2 i , z 2 = 3 − i . Tìm số phức z = z 2 z 1
A. z = 1 10 + 7 10 i
B. z = 1 5 + 7 5 i
C. z = 1 5 − 7 5 i
D. z = − 1 10 + 7 10 i
Đáp án C.
Ta có
z = z 2 z 1 = 3 − i 1 + 2 i = 3 − i 1 − 2 i 1 + 2 i 1 − 2 i = 1 − 7 i 5 = 1 5 − 7 5 i
Đúng 0
Bình luận (0)
Cho số phức
z
a
+
b
i
thỏa mãn
3
a
-
2
b
12
. Gọi
z
1
,
z
2
là hai số phức thỏa mãn
z
1
-
3
-
4
i
và
2
z
2...
Đọc tiếp
Cho số phức z = a + b i thỏa mãn 3 a - 2 b = 12 . Gọi z 1 , z 2 là hai số phức thỏa mãn z 1 - 3 - 4 i và 2 z 2 - 6 - 8 i . Giá trị nhỏ nhất của biểu thức P = z - z 1 + z - 2 z 2 + 2 bằng
A. 9 - 3 2
B. 9945 13
C. 9 + 3 2
D. 9945 31
Cho hai số phức z1 3i - 4; z2 3 - i. Tìm số phức z z1 – z2. A. 6 - 5i B. 7 + 4i C. 4 + 4i D. -7 + 4i
Đọc tiếp
Cho hai số phức z1 = 3i - 4; z2 = 3 - i. Tìm số phức z = z1 – z2.
A. 6 - 5i
B. 7 + 4i
C. 4 + 4i
D. -7 + 4i
Chọn D.
Ta có z1 - z2 = (-4 + 3i) - ( 3 - i) = -7 + 4i.
Đúng 0
Bình luận (0)