Chọn D.
Ta có z1 - z2 = (-4 + 3i) - ( 3 - i) = -7 + 4i.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
a) Cho hai số phức z1 = 1 + 2i ; z2 = 2 – 3i . Xác định phần thực và phần ảo của số phức z1 – 2z2 .
b) Cho hai số phức z1 = 2 + 5i ; z2 = 3 – 4i . Xác định phần thực và phần ảo của số phức z1.z2
Cho hai số phức z1 2 - 3i; z2 4i - 10 số phức z z1 – z2. A. z 3 + 3i. B. z 12 - 7i. C. z 2 - 3i. D. z 3 - i.
Đọc tiếp
Cho hai số phức z1 = 2 - 3i; z2 = 4i - 10 số phức z = z1 – z2.
A. z = 3 + 3i.
B. z = 12 - 7i.
C. z = 2 - 3i.
D. z = 3 - i.
Cho các số phức z,
z
1
,
z
2
thỏa mãn
|
z
1
-
4
-
5
i
|
|
z
2
-
1
|
và
z
¯
+
4
i...
Đọc tiếp
Cho các số phức z, z 1 , z 2 thỏa mãn | z 1 - 4 - 5 i | = | z 2 - 1 | và z ¯ + 4 i = z - 8 + 4 i . Tính M = | z 1 - z 2 | khi P = | z - z 1 | + | z - z 2 | đạt giá trị nhỏ nhất.
Cho hai số phức z11+3i và z23-4i. Môđun của số phức wz1/z2 là A. . B. C. . D..
Đọc tiếp
Cho hai số phức z1=1+3i và z2=3-4i. Môđun của số phức w=z1/z2 là
A. 
.
B. 
C. 
.
D.
.
Cho hai số phức z 1 = 2 + 5i ; z 2 = 3 – 4i . Xác định phần thực và phần ảo của số phức z 1 . z 2
Cho hai số phức
z
1
2 + 4i và
z
2
1 - 3i. Tính môđun của số phức
z
1
+ 2i
z
2
A. |
z
1
+ 2i
z
2
| 8 B. |
z
1
+ 2i
z...
Đọc tiếp
Cho hai số phức z 1 = 2 + 4i và z 2 = 1 - 3i. Tính môđun của số phức z 1 + 2i z 2
A. | z 1 + 2i z 2 | = 8
B. | z 1 + 2i z 2 | = 10
C. | z 1 + 2i z 2 | = 1
D. | z 1 + 2i z 2 | = 10
Cho hai số phức
z
1
-
2
-
3
i
;
z
2
1
+
4
i
.
T
í
n
h
z
1
.
z
2
A. -14 - 8i B. 10 + 11i C. 10 - 11i D. –14 + 11i
Đọc tiếp
Cho hai số phức z 1 = - 2 - 3 i ; z 2 = 1 + 4 i . T í n h z 1 . z 2
A. -14 - 8i
B. 10 + 11i
C. 10 - 11i
D. –14 + 11i
Biết rằng hai số phức
z
1
,
z
2
thỏa mãn
|
z
1
-
3
-
4
i
|
1
và
|
z
2
-
3
-
4
i
|
1
2
. Số phức z có phần thực là a v...
Đọc tiếp
Biết rằng hai số phức z 1 , z 2 thỏa mãn | z 1 - 3 - 4 i | = 1 và | z 2 - 3 - 4 i | = 1 2 . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3 a - 2 b = 12 . Giá trị nhỏ nhất của P = | z - z 1 | + | z - 2 z 2 | + 2 bằng:
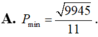
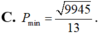
Cho hai số phức z 1 = 4 - 3i và z 2 = 7 + 3i. Tìm số phức z = z 1 - z 2
A. z = 11
B. z = 3 + 6i
C. z = -1 - 10i
D. z = -3 - 6i
Cho hai số phức
z
1
2
+
3
i
,
z
2
-
4
-
5
i
. Số phức
z
z
1
+
z
2
là:
Đọc tiếp
Cho hai số phức z 1 = 2 + 3 i , z 2 = - 4 - 5 i . Số phức z = z 1 + z 2 là:
