Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, A C = 2 a 3 , B D = 2 a , hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O đến (SAB) bằng a 3 4 . Thể tích của khối chóp S.ABCD là:
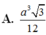
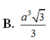
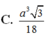
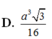
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, cạnh SAL(ABCD). Biết St= a/3, BAD = 1200. a) Chứng minh (SIC)L(SBD). b) Tính góc giữa SC với mặt phẳng (ABCD). c) Tính góc giữa hai mặt phẳng (SBC) và (ABCD). d) Tính khoảng cách giữa tôi và SC. c) "Gọi 7 là điểm bất kì thuộc đoạn thẳng $4. Dung thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng đi qua và vuông góc với St. Tìm vị trí điểm P để diện tích thiết diện thu được bằng một nửa diện tích hình thoi ABCD.
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: (SC;(ABCD))=(CS;CA)=góc SCA
Xét ΔBAC có BA=BC vàgóc BAC=60 độ
nên ΔBAC đều
=>AC=a
=>\(SC=\sqrt{SA^2+AC^2}=\dfrac{\sqrt{10}}{3}\cdot a\)
tan SCA=SA/AC=1/3
=>góc SCA=18 độ
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAC ^ = 60 ° , SO ⊥ ( ABCD ) và SO = 3a/4. Tính thể tích khối chóp S.ABCD.
A. a 3 3 8
B. a 3 3 4
C. a 3 4
D. 3 a 3 3 8
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB = a, B A D ^ = 60 0 , S O ⊥ A B C D và mặt phẳng (SCD) tạo với đáy một góc 60 0 . Tính thế tích khối chóp S.ABCD.
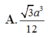
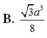
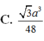
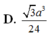
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB = a, ∠ B A D = 60 0 , S O ⊥ ( A B C D ) và mặt phẳng (SCD) tạo với đáy một góc 60 0 . Tính thế tích khối chóp S.ABCD.
A. 3 a 3 12
B. 3 a 3 8
C. 3 a 3 48
D. 3 a 3 24
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB=a, B A D ^ = 60 ° SO ⊥ (ABCD) và mặt phẳng (SCD) tạo với mặt đáy một góc 60 ° . Tính thể tích khối chóp S.ABCD
A. V S . A B C D = 3 a 3 12
B. V S . A B C D = 3 a 3 24
C. V S . A B C D = 3 a 3 8
D. V S . A B C D = 3 a 3 48
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, A C = 2 a 3 , B D = 2 a . Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD). Biết khoảng cách từ tâm O đến (SAB) bằng a 3 4 tính thể tích V của khối chóp S.ABCD theo a.
A. V = a 2 3
B. V = a 3 3 3
C. V = a 3 3 9
D. V = a 3 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc A bằng 60 o , O là tâm hình thoi, SA vuông góc với đáy. Góc giữa SO và mặt phẳng đáy bằng 45 o . Tính theo a thể tích khối chóp SABCD.
A. 3 2 a 3 x
B. a 3 4
C. 3 a 3 8
D. 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh bằng 2, ABC ^ = 60 0 . Biết SO ⊥ ABCD và thể tích khối chóp S.ABCD bằng 2. Tính SA.
A. SA = 3
B. SA = 2
C. SA = 1
D. SA = 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAD = 60 ° với AC cắt BD tại O, SO ⊥ ( ABCD ) và SO = 3a/4. Tính thể tích khối chóp S.ABCD.
Lời giải:
$\widehat{BAD}=60^0\Rightarrow \widehat{BAO}=30^0$
$\frac{BO}{AB}=\sin \widehat{BAO}=\sin 30^0=\frac{1}{2}$
$\Rightarrow BO=\frac{AB}{2}=\frac{a}{2}$
$BD=2BO=a$
$\frac{AO}{AB}=\cos \widehat{BAO}=\cos 30^0=\frac{\sqrt{3}}{2}$
$\Rightarrow AO=\frac{\sqrt{3}a}{2}$
$\Rightarrow AC=\sqrt{3}a$
$S_{ABCD}=\frac{BD.AC}{2}=\frac{\sqrt{3}a^2}{2}$
$V_{S.ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.\frac{3a}{4}.\frac{\sqrt{3}a^2}{2}=\frac{\sqrt{3}a^3}{8}$
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, A B = a , B A D ^ = 60 ° , S O ⊥ A B C D và mặt phẳng (SCD) tạo với mặt đáy một góc 60 ° . Tính thể tích khối chóp
A. V S . A B C D = 3 a 3 24
B. V S . A B C D = 3 a 3 8
C. V S . A B C D = 3 a 3 12
D. V S . A B C D = 3 a 3 48