Có tất cả bao nhiêu giá trị nguyên của m để hàm số f x = 8 3 x + 1 − 2 x 2 − 1 k h i x > 1 m 3 x 2 − m − 3 x k h i x ≤ 1 có giới hạn tại x = 1.
A. 1
B. 2
C. 3
D. 0
Những câu hỏi liên quan
4 tháng 1 2022 lúc 21:19
Cho hàm số f(x) = (m - 1)x3 - 5x2 + (m+3)x + 3. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = f(\(\left|x\right|\)) có đúng 3 điểm cực trị?
- Với \(m=1\) thỏa mãn
- Với \(m\ne1\):
\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)
\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương
TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)
TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu
\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)
\(\Rightarrow-3< m< 1\)
Vậy \(-3< m\le1\)
Đúng 2
Bình luận (0)
Cho hàm số y
(
m
-
1
)
x
3
-
5
x
2
+
(
m
+
3
)
x
+
3
. Có tất cả bao nhiêu giá trị nguyên của m để hàm số yf(|x|) có đúng 3 điểm cực trị? A. 5. B. 3. C. 4. D. 0.
Đọc tiếp
Cho hàm số y = ( m - 1 ) x 3 - 5 x 2 + ( m + 3 ) x + 3 . Có tất cả bao nhiêu giá trị nguyên của m để hàm số y=f(|x|) có đúng 3 điểm cực trị?
A. 5.
B. 3.
C. 4.
D. 0.
Cho hàm số
f
(
x
)
m
-
1
x
3
-
5
x
2
+
m
+
3
x
+
3
. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số
y
...
Đọc tiếp
Cho hàm số f ( x ) = m - 1 x 3 - 5 x 2 + m + 3 x + 3 . Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = f x có đúng 3 điểm cực trị?
A. 1.
B. 5.
C. 3.
D. 4.
Cho hàm số y f(x) có bảng biến thiên:Có tất cả bao nhiêu giá trị nguyên của m không vượt quá 10 để bất phương trình
f
log
2
10
−
x
−
x
−
6
≤
m
có nghiệm? A. 1...
Đọc tiếp
Cho hàm số y = f(x) có bảng biến thiên:
Có tất cả bao nhiêu giá trị nguyên của m không vượt quá 10 để bất phương trình f log 2 10 − x − x − 6 ≤ m có nghiệm?
A. 15.
B. 16.
C. 17.
D. 14.
Cho hàm số
y
(
m
-
1
)
x
3
-
5
x
2
+
(
m
+
3
)
x
+
3
. Có tất cả bao nhiêu giá trị nguyên của m để hàm số
y
f
x
có đúng 3 điểm cực trị? A. 5 B. 3 C. 4 D. 0
Đọc tiếp
Cho hàm số y = ( m - 1 ) x 3 - 5 x 2 + ( m + 3 ) x + 3 . Có tất cả bao nhiêu giá trị nguyên của m để hàm số y = f x có đúng 3 điểm cực trị?
A. 5
B. 3
C. 4
D. 0
Để hàm số 
có đúng 3 cực trị thì hàm số 
có 2 cực trị trái dấu.
Trước hết cần điều kiện m-1≠0
⇔m≠1
Ta có 
Để hàm số
có 2 cực trị trái dấu thì phương trình y'=0 có 2 nghiệm trái dấu 
Kết hợp điều kiện 
Khi m=1 thì hàm số trở thành 
có 1 cực trị Khi đó hàm số 
có đúng 3 điểm cực trị.
Vậy m∈-2;-1;0;1
Chọn C
Đúng 0
Bình luận (0)
Trong tất cả các giá trị của m để đồ thị hàm số
y
x
−
4
m
x
2
+
m
2
−
17
có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên A. 1. B. 2. C. 3. D. 4.
Đọc tiếp
Trong tất cả các giá trị của m để đồ thị hàm số y = x − 4 m x 2 + m 2 − 17 có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên
A. 1.
B. 2.
C. 3.
D. 4.
Trong tất cả các giá trị của m để đồ thị hàm số
y
x
−
4
m
x
2
+
m
2
−
17
có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Trong tất cả các giá trị của m để đồ thị hàm số y = x − 4 m x 2 + m 2 − 17 có bốn đường tiệm cận, có bao nhiêu giá trị m nguyên?
A. 1
B. 2
C. 3
D. 4
Cho hàm số \(y=-2x^3+(2m-1)x^2-(m^2-1)x+2\). Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có hai điểm cực trị?
\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)
Hàm có 2 cực trị khi:
\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)
\(\Rightarrow-2m^2-4m+7>0\)
\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)
\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)
Đúng 2
Bình luận (0)
Cho hàm số
y
f
(
x
)
thỏa mãn
lim
x
→
-
∞
f
(
x
)
2019
m
,
lim
x
→
+
∞
f
(
x
)
2020
m
4...
Đọc tiếp
Cho hàm số y = f ( x ) thỏa mãn lim x → - ∞ f ( x ) = 2019 m , lim x → + ∞ f ( x ) = 2020 m 4 (với m là tham số thực). Hỏi có tất cả bao nhiêu giá trị của m để đồ thị của hàm số y = f ( x ) có duy nhất một tiệm cận ngang?
A. 4
B. 2
C. 3
D. 1
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = 1 3 x 3 − 1 2 m x 2 + x + 2018 đồng biến trên R?
A. 5
B. 3
C. 4
D. 2
Đáp án A
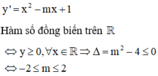
Suy ra có 5 giá trị nguyên của m thỏa mãn đề bài
Đúng 0
Bình luận (0)