Cho hai số phức z và w khác 0 thoả mãn z + 3 w = 5 w và z - 2 w i = z - 2 w - 2 w i . Phần thực của số phức z w bằng
A. 1.
B. −3.
C. −1.
D. 3.
Cho hai số phức z và w khác 0 thoả mãn|z+3w|=5|w| và |z-2wi|=|z-2w-2wi| Phần thực của số phức z/w bằng
A.1.
B.-3.
C.-1.
D.3
Cho hai số phức z,w khác 0 thoả mãn |z|=|w|= 3 2 , |z-iw|>0. Phần ảo của số phức z w bằng
A.- 4 2 9
B. -7/9.
C. 4 2 9
D. 7/9
Cho hai số phức z,w khác 0 thoả mãn |z|=|w|= 3 2 , |z-iw|>0. Phần ảo của số phức z w bằng
A.- 4 2 9
B. -7/9.
C. 4 2 9
D. 7/9
Cho hai số phức z và w thoả mãn z+2w=8+6i và z - w = 4 . Giá trị lớn nhất của biểu thức z + w bằng
A. 4 6
B. 2 26
C. 66
D. 3 6
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w|. Phẩn thực của số phức u = z w là:
A. a = 1 4
B. a = 1
C. a = 1 8
D. a = - 1 8
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w| Phẩn thực của số phức u = z w là:
![]()
![]()
![]()
![]()
Cho các số phức \(z_1\), \(z_2\) thoả mãn \(\left|z-2\right|=\left|z\right|\) và \(\left|z_2-z_1\right|=4\). Số phức \(w\) thoả mãn \(\left|w-3-5i\right|=1\), số phức \(u\) thoả mãn \(\left|u-4+4i\right|=2\). Giá trị nhỏ nhất của \(T=\left|w-z_2\right|+\left|u-z_1\right|\) là
A. \(5\sqrt{3}-3\) B. \(5\sqrt{2}-3\) C. \(2\sqrt{5}-3\) D. \(5\sqrt{3}-2\)
Cho các số phức z, w khác 0 thỏa mãn z+w khác 0 và 1 z + 3 w = 6 z + w Khi đó z w bằng
![]()
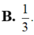
![]()
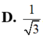
Cho các số phức z, w khác 0 thỏa mãn z + w ≠ 0 và 1 z + 3 w = 6 z + w . Khi đó z w bằng
A. 3
B. 1 3
C. 3
D. 1 3