Trong không gian Oxyz, cho mặt cầu (S): x - 1 2 + y + 2 2 + ( z - 5 ) 2 = 9 . Phương trình nào dưới đây là phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) tại điểm A(2;-4;3)?

A. x – 6y + 8z – 50 = 0

B. x – 2y – 2z – 4 = 0

C. x – 2y – 2z + 4 = 0

D. 3x – 6y + 8z – 54 = 0

Trong không gian với hệ toạ độ Oxyz,  cho mặt cầu (S) có phương trình:  x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0   . Viết phương trình mặt phẳng (P) song song với giá của véc tơ  v ⇀ = 1 ; 6 ; 2 , vuông góc với mặt phẳng  ( α ) :   x + 4 y + z - 11 = 0  và tiếp xúc với (S).

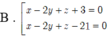
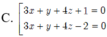
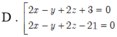
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S) có phương trình:  x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0   . Viết phương trình mặt phẳng (P) song song với giá của véc tơ  v ⇀ = 1 ; 6 ; 2 , vuông góc với mặt phẳng  ( α ) :   x + 4 y + z - 11 = 0  và tiếp xúc với (S).

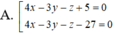
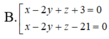
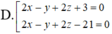
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x 2 +   y 2   +   z 2 = 1. Viết phương trình mặt phẳng (P) đi qua 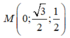 và tiếp xúc với (S)

A.  3 x + 4z - 2 = 0

B.  3 y + z - 2 = 0

C. y +  3 z = 0

D. x +  3 y + z - 2 = 0

Trong không gian Oxyz, cho mặt cầu (S):

x - 1 2 + y + 2 2 + z - 5 2 = 9  . Phương trình nào dưới đây là phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) tại điểm A(2;-4;3)?

A. x – 6y + 8z – 50 = 0

B. x – 2y – 2z – 4 = 0

C. x – 2y – 2z + 4 = 0

D. 3x – 6y + 8z – 54 = 0

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x 2 = y - 3 1 = z - 2 1   và hai mặt phẳng

P x - 2 y + 2 z = 0 ;   Q :   x - 2 y + 3 z - 5 = 0 . Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).

A.  S :   x + 2 2 + y + 4 2 + z + 3 2 = 1

B. S :   x - 2 2 + y - 4 2 + z - 3 2 = 6

C. S :   x - 2 2 + y - 4 2 + z - 3 2 = 2 7

D. S :   x - 2 2 + y + 4 2 + z + 4 2 = 8