Cho hình nón tròn xoay có đường cao h = 20 c m . Gọi 2 α là góc ở đỉnh của hình nón với tan α = 3 4 . Độ dài đường sinh của hình nón là
A. 25cm
B. 35cm
C. 15cm
D. 45cm
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Gọi I là một điểm trên đường cao DO của hình nón sao cho DI DO = k (0 < k < 1) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
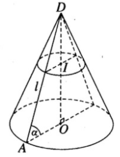
Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’
với 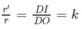
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
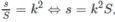
trong đó S = πr 2 = πl 2 cos 2 α
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s = k 2 s = k 2 πl 2 cos 2 α
Cho hình nón tròn xoay có chiều cao h = 20 cm, bán kính đáy r = 25 cm.. Mặt phẳng ( α ) đi qua đỉnh của hình nón cách tâm của đáy 12 cm Tính diện tích thiết diện của hình nón cắt bởi mặt phẳng ( α ) .
A. S = 400 ( c m 2 )
B. S = 406 ( c m 2 )
C. S = 300 ( c m 2 )
D. S = 500 ( c m 2 )
Cho hình nón tròn xoay có bán kính đáy R, chiều cao h và góc ở đỉnh là góc ( α ) không là góc nhọn. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác. Khi đó tam giác có diện tích lớn nhất là
A. 1 2 ( h 2 + R )
B. 1 2 ( h 2 + R ) π
C. 1 2 ( h 2 + R 2 ) h
D. 1 2 ( h 2 - R 2 )
Cho hình nón tròn xoay có bán kính đáy R, chiều cao h và góc ở đỉnh là góc α không là góc nhọn. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác. Khi đó tam giác có diện tích lớn nhất là:
A. 1 2 ( h 2 + R 2 )
B. 1 2 ( h 2 + R ) π
C. 1 2 ( h + R 2 ) h
D. 1 2 ( h 2 - R 2 )
Đáp án A
Giả sử thiết diện là một tam giác cân có độ dài chiều cao hạ từ đỉnh nón xuống đáy tam giác là x ( 0 < x < R 2 + h 2 )
Khi đó ta dễ dàng tính được độ dài đáy tam giác theo x, h và R là:
2 R 2 + h 2 - x 2
Do đó, diện tích S của tam giác là:
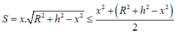 (BĐT Cauchy)
(BĐT Cauchy)
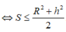
Vậy S m a x = R 2 + h 2 2
Cho hình nón tròn xoay có chiều cao h = 20 c m , bán kính đáy r = 25 c m . Mặt phẳng α đi qua đỉnh của hình nón cách tâm của đáy 12cm Tính diện tích thiết diện của hình nón cắt bởi mặt phẳng α
A. S = 400 c m 2
B. S = 406 c m 2
C. S = 300 c m 2
D. S = 500 c m 2
Đáp án D
Ta có: 1 d 2 I ; α = 1 d 2 + 1 h 2 trong đó d là khoảng cách từ tâm của đáy đến giao tuyến của α và đáy.
Khi đó d = 15 ⇒ độ dài dây cung a = 2 r 2 − d 2 = 40 ; đường cao thiết diện = h 2 + d 2 = 25
Do đó A = 1 2 a . h ' = 1 2 .40.25 = 500 c m 2 .
Cho hình chóp S.ABCD có AB = a, mặt bên tọa với đáy một góc 45 ° . Một khối nón có đỉnh là S, đáy là hình tròn ngoại tiếp hình vuông ABCD. Gọi α là góc ở định của hình nón. Tính cosα
A. cos α = - 1 3
B. cos α = 3 3
C. cos α = 6 3
D. cos α = 1 3
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Tính diện tích xung quanh của hình nón và thể tích khối nón được tạo nên.
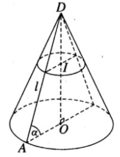
Gọi r là bán kính của đường tròn đáy.
Ta có OA = r = l.cos α (với O là tâm của đường tròn đáy và A là một điểm trên đường tròn đó).
Ta suy ra: S xq = πrl = πl 2 cosα
Khối nón có chiều cao h = DO = lsin α . Do đó thể tích V của khối nón được tính theo công thức
![]()
Vậy :
![]()
Cho hình trụ trục OO', đường tròn đáy (C) và (C'). Xét hình nón đỉnh O', đáy (C) có đường sinh hợp với đáy góc α ( 0 ∘ < α 90 ∘ ) . Cho biết tỉ số diện tích xung quanh của hình lăng trụ và hình nón bằng 3 . Tính giá trị α .
A. 30 ∘ .
A. 45 ∘ .
C. 60 ∘ .
A. Kết quả khác
Cho S.ABC là hình chóp tam giác đều có các cạnh bên bằng a và có góc giữa các mặt bên và mặt phẳng đáy là α. Hình nón đỉnh S có đường tròn đáy nội tiếp tam giác đều ABC gọi là hình nón nội tiếp hình nón đã cho. Hãy tính diện tích xung quanh của hình nón này theo a và α
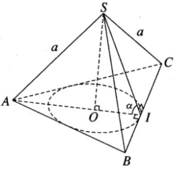
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và

Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy 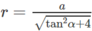
Hình nón nội tiếp có đường sinh là :
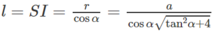
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
![]()