Viết phương trình đường thẳng d song song với ∆ : x + 4 3 = y - 5 - 4 = z + 2 1 và cắt hai đường thẳng d 1 : x - 1 3 = y - 2 1 = z - 6 5 , d 2 = x - 6 3 = y 2 = z - 1 1
![]()
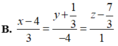

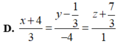
Viết phương trình đường thẳng d đi qua điểm M(3;-4) và song song với đường thẳng (d’): \(\left\{{}\begin{matrix}x=2-t\\y=-1+6t\end{matrix}\right.\)
- Đường thẳng (d, ) có : \(\overrightarrow{u}\left(-1;6\right)\)
Mà (d) song song với (d,)
=> \(\overrightarrow{u}\left(-1;6\right)\) là vecto chỉ phương của (d)
=> Phương trình tham số của (d) là :
\(\left\{{}\begin{matrix}x=3-t\\y=-4+6t\end{matrix}\right.\) \(\left(t\in R\right)\)
Vậy ...
Cho hàm số y = 2x - 3 có đồ thị (d) và điểm A( -1;- 5).
a) Viết phương trình đường thẳng d1 qua A và song song với trục Ox .
b) Viết phương trình đường thẳng d2 qua A và song song với đường thẳng d .
c) Viết phương trình đường thẳng d3 qua A và vuông góc với đường thẳng d .
d) Viết phương trình đường thẳng d4 qua A và gốc tọa độ
GIÚP MÌNH VỚI, MÌNH ĐANG CẦN GẤP
Gọi các đồ thị có CT chung là \(ax+b\)
\(a,\Leftrightarrow\left\{{}\begin{matrix}-a+b=-5\\a=0;b\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-5\end{matrix}\right.\Leftrightarrow\left(d_1\right):y=-5\\ b,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\a=2;b\ne-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=7\end{matrix}\right.\Leftrightarrow\left(d_2\right):y=2x+7\\ c,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\2a=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=3\end{matrix}\right.\Leftrightarrow\left(d_3\right):y=-2x+3\\ d,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-5\\b=0\end{matrix}\right.\Leftrightarrow\left(d_4\right):y=-5x\)
Trong Oxy cho M(1;4) N(-3;-5) P(3;-4) và đường thẳng d: 3x-4y+6=0 a) Viết phương trình đường thẳng delta đi qua M và song song với d b) Viết phương trình đường thẳng delta đi qua N và vuông góc với d
a: Vì Δ//d nên Δ: 3x-4y+c=0
Thay x=1 và y=4 vào Δ, ta được:
c+3-16=0
=>c=13
b: Vì Δ vuông góc d nên Δ: 4x+3y+c=0
Thay x=-3 và y=-5 vào Δ, ta được:
c+4*(-3)+3(-5)=0
=>c-27=0
=>c=27
=>4x+3y+27=0
Viết phương trình đường thẳng song song với đường thẳng d:\(\left\{{}\begin{matrix}x=3-2t\\y=1+3t\end{matrix}\right.\)
Chắc là đề bài thiếu dữ kiện, do có vô số đường thẳng song song với d, tất cả những đường thẳng có dạng \(3x+2y+c=0\) với \(c\ne-11\) đều thỏa mãn yêu cầu
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
Bài 5. Trong mặt phẳng Oxy, cho điểm A(2;-1) và đường thẳng d : 3x-4y+5=0
a) Viết phương trình đường thẳng đi qua A và vuông góc với d
b) Viết phương trình đường thẳng đi qua A và song song với d.
c) Viết phương trình đường thẳng song song với d và cách A một khoảng bằng 3
Gọi đường thẳng đi qua A là d'.
a) Ta có: \(d'\perp d.\)
\(\Rightarrow\) VTPT của d là VTCP của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\overrightarrow{u_{d'}}=\left(3;-4\right).\Rightarrow\overrightarrow{n_{d'}}=\left(4;3\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(4\left(x-2\right)+3\left(y+1\right)=0.\\ \Leftrightarrow4x+3y-5=0.\)
b) Ta có: \(d'//d.\)
\(\Rightarrow\) VTPT của d là VTPT của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\) \(\overrightarrow{n_{d'}}=\left(3;-4\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(3\left(x-2\right)-4\left(y+1\right)=0.\\ \Leftrightarrow3x-4y-10=0.\)
Trong mặt phẳng tọa độ Oxy cho m điểm M 1,0 và đường thẳng d :x -4y +5=0. a ,viết phương trình đường thẳng d qua m và song song với đường thẳng d x - 4y + 5 = 0 b,viết phương trình đường thẳng d qua m và vuông góc với đường thẳng d x - 4y + 5 = 0 , C,Viết phương trình đường tròn {C} M và tiếp xúc với đường thẳng d x - 4y + 5 = 0
a: Vì (d)//x-4y+5=0 nên (d): x-4y+c=0
Thay x=1 và y=0 vào (d), ta được:
c+1=0
=>c=-1
=>x-4y-1=0
b: Vì (d) vuông góc x-4y+5=0
nên (d): 4x+y+c=0
Thay x=1 và y=0 vào (d), ta được:
c+4=0
=>c=-4
=>4x+y-4=0
Viết phương trình đường thẳng (d) đi qua A(1;4) và song song với đường thẳng (d'): y= x+7
Vì : (d) song song với đường thẳng (d') : y= x + 7
=> (d) có dạng : y = x + b
Vì (d) đi qua A(1,4) :
=> 4 = 1 + b
=> b = 3
(d) ; y = x + 3
`d////d' => d` có dạng: `y=x+b`
`A(1;4) \in d <=> 4=1+b<=>b=3`
`=>d : y=x+3`.
Cho: (d): y = 2x + 3; (d’): y = - 3x - 2
a/ Xác định tọa độ giao điểm A của (d) và (d’)
b/ Viết phương trình đường thẳng đi qua A và song song với đường thẳng y = - x + 5
c/ Viết phương trình đường thẳng đi qua A và có hoành độ luôn bằng tung độ
d/ Viết phương trình đường thẳng đi qua A và cắt trục tung tại điểm có tung độ bằng -1
e/ Viết phương trình đường thẳng đi qua A và vuông với trục hoành
f/ Vẽ (d) và (d’) trên cùng một hệ trục tọa độ. Giao điểm của (d) và (d’) với trục hoành lần lượt là B; C. Tính diện tích tam giác ABC?
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=-3x-2\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)
Cho: (d): y = 2x + 3; (d’): y = - 3x - 2
a/ Xác định tọa độ giao điểm A của (d) và (d’)
b/ Viết phương trình đường thẳng đi qua A và song song với đường thẳng y = - x + 5
c/ Viết phương trình đường thẳng đi qua A và có hoành độ luôn bằng tung độ
d/ Viết phương trình đường thẳng đi qua A và cắt trục tung tại điểm có tung độ bằng -1
e/ Viết phương trình đường thẳng đi qua A và vuông với trục hoành
f/ Vẽ (d) và (d’) trên cùng một hệ trục tọa độ. Giao điểm của (d) và (d’) với trục hoành lần lượt là B; C. Tính diện tích tam giác ABC?
\(a,\text{PT hoành độ giao điểm: }2x+3=-3x-2\Leftrightarrow x=-1\Leftrightarrow y=1\Leftrightarrow A\left(-1;1\right)\\ b,\text{Gọi đt đó là }y=ax+b\\ \Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\a=-1;b\ne5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\Leftrightarrow y=-x\\ d,\text{Gọi đt cần tìm là }y=ax+b\\ \Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\Leftrightarrow y=-2x-1\)