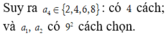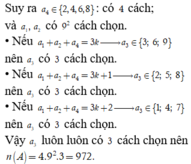Chọn ngẫu nhiên 6 số từ tập M = 1 ; 2 ; 3 ; 4 ; . . . ; 2018 . Xác suất để chọn được 6 số lập thành cấp số nhân tăng có công bội là một số nguyên dương bằng
A. 36 C 2018 6
B. 64 C 2018 6
C. 72 C 2018 6
D. 2018 C 2018 6
Những câu hỏi liên quan
Gọi S là tập hợp các số tự nhiên có 6 chữ số được lập từ tập hợp \(A=\left\{0;1;2;3;4;5;6\right\}\). Chọn ngẫu nhiên 1 số từ tập hợp S . Tính xác suất để chọn được số tự nhiên có tích các chữ số bằng 120.
cho A là tập hợp các số tự nhiên có 10 chữ số được lấy từ tập M={0;1;2;3;4;5;6} ( các chữ số có thể giống nhau). Chọn ngẫu nhiên một số thuộc A, tính xác suất số được chọn chia hết cho 6
Tập S gồm các số tự nhiên có 6 chữ số khác nhau được thành lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8. Chọn ngẫu nhiên một số từ tập S. Xác suất để số được chọn không có hai chữ số chẵn đứng cạnh nhau là: A.
11
70
B.
29
140
C.
13
80
D.
97
560
Đọc tiếp
Tập S gồm các số tự nhiên có 6 chữ số khác nhau được thành lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8. Chọn ngẫu nhiên một số từ tập S. Xác suất để số được chọn không có hai chữ số chẵn đứng cạnh nhau là:
A. 11 70
B. 29 140
C. 13 80
D. 97 560
cho tập hợp A = (0,1,2,3,4,5,6) gọi S là tập hợp các số tự nhiên có 4 chữ số đôi 1 khác nhau được lập từ tập A. chọn ngẫu nhiên 1 số từ S tính xác suất là chẵn luôn có 1 số 6
Xem chi tiết
Gọi A là tập hợp tất cả các số tự nhiên gồm bốn chữ số đôi một khác nhau được chọn từ các chữ số 1; 2; 3; 4; 5; 6. Chọn ngẫu nhiên một số từ tập A. Xác suất để số chọn được là số chia hết cho 5 là A. 2/3 B. 1/6 C. 1/30 D. 5/6
Đọc tiếp
Gọi A là tập hợp tất cả các số tự nhiên gồm bốn chữ số đôi một khác nhau được chọn từ các chữ số 1; 2; 3; 4; 5; 6. Chọn ngẫu nhiên một số từ tập A. Xác suất để số chọn được là số chia hết cho 5 là
A. 2/3
B. 1/6
C. 1/30
D. 5/6
Gọi
A
là tập hợp tất cả các số tự nhiên gồm bốn chữ số đôi một khác nhau được chọn từ các chữ số
1
;
2
;
3
;
4
;
5
;
6
. Chọn ngẫu nhiên một số từ tập
A
. Xác suất để số chọn được là số chia hết cho
5
là A.
2
3
. B.
1...
Đọc tiếp
Gọi A là tập hợp tất cả các số tự nhiên gồm bốn chữ số đôi một khác nhau được chọn từ các chữ số 1 ; 2 ; 3 ; 4 ; 5 ; 6 . Chọn ngẫu nhiên một số từ tập A . Xác suất để số chọn được là số chia hết cho 5 là
A. 2 3 .
B. 1 6 .
C. 1 30 .
D. 5 6 .
Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số được lập từ tập hợp X {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ S. Tính xác suất chọn được số chia hết cho 6 A.
4
27
B.
9
28
C.
6
23
D.
15
31
Đọc tiếp
Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số được lập từ tập hợp X = {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ S. Tính xác suất chọn được số chia hết cho 6
A. 4 27
B. 9 28
C. 6 23
D. 15 31
Chọn A
+ Ta có 
Ta có d có 4 cách chọn {2;4;6;8}, a có 9 cách chọn, b có 9 cách chọn. Vì a + b + d khi chia cho 3 có 3 khả năng số dư
{0;1;2}, mà 
nên c có 3 cách chọn.
Ta có: 
Xác suất cần tìm là: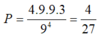 
Đúng 0
Bình luận (0)
câu 1 cho A là tập hợp các số có hai chữ số khác nhau có bao nhiêu cách chọn ngẫu nhiên ba số từ tập a
câu 2 cho A là tập hợp các số có ba chữ số khác nhau có bao nhiêu cách chọn ngẫu nhiên hai số từ tập a
Câu 1:
Gọi số tổng quát là \(X=\overline{ab}\)
a có 9 cách chọn
b có9 cách chọn
=>Có 9*9=81(số)
Số cách chọn ngẫu nhiên 3 số từ tập A là \(C^3_{81}\left(cách\right)\)
Câu 2:
\(\overline{abc}\)
a có 9 cách
b có 9 cách
c có 8 cách
=>có 9*9*8=81*8=648(số)
Số cách chọn ngẫu nhiên 2 số từ tập A là \(C^2_{648}\left(cách\right)\)
Đúng 2
Bình luận (1)
`C1: n(A)=9.9=81`
`=>` Có `C_81 ^3 =85320` cách chọn `3` số ngẫu nhiên từ `A.`
`C2: n(A)=9.9.8=648`
`=>` Có `C_648 ^2 =209628` cách chọn `2` số ngẫu nhiên từ `A.`
Đúng 1
Bình luận (0)
Cho tập hợp
A
1
;
2
;
3
;
4
;
5
;
6
;
7
;
8
;
9
. Gọi S là tập hợp các số tự nhiên có 4 chữ số được lập từ các chữ số thuộc tập A. Chọn ngẫu nhiên một số từ S, xác suất để số được chọn chia hết cho 6 bằng A. ...
Đọc tiếp
Cho tập hợp A = 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 . Gọi S là tập hợp các số tự nhiên có 4 chữ số được lập từ các chữ số thuộc tập A. Chọn ngẫu nhiên một số từ S, xác suất để số được chọn chia hết cho 6 bằng
A. 1 9
B. 4 9
C. 4 27
D. 9 28
Tập S có 9 4 phần tử. Ta có
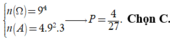
Thật vậy: Gọi số thỏa mãn biến cố là 
Đúng 0
Bình luận (0)