Giả sử tích phân I = ∫ 1 5 1 1 + 3 x + 1 d x = a + b . ln 3 + c . ln 5 . Lúc đó:
A. a + b + c = 4 3
B. a + b + c = 5 3
C. a + b + c = 7 3
D. a + b + c = 8 3
Những câu hỏi liên quan
Cho tích phân
I
∫
0
1
x
7
1
+
x
2
5
, giả sử đặt
t
1
+
x
2
. Tìm mệnh đề đúng. A.
I...
Đọc tiếp
Cho tích phân I = ∫ 0 1 x 7 1 + x 2 5 , giả sử đặt t = 1 + x 2 . Tìm mệnh đề đúng.
A. I = 1 2 ∫ 1 2 t - 1 3 t 3 d t
B. I = ∫ 1 3 t - 1 3 t 3 d t
C. I = 1 2 ∫ 1 2 t - 1 3 t 4 d t
D. I = 3 2 ∫ 1 4 t - 1 3 t 4 d t
SGK Ngữ văn 10 Chân trời sáng tạo tập 2 trang 39
6 tháng 5 2023 lúc 16:09
5. Phân tích cách sử dụng lí lẽ và bằng chứng của tác giả trong phần 1 hoặc phần 2 của bài cáo.
Phương pháp giải:
- Đọc kĩ phần 1 hoặc phần 2.
- Chú ý các lí lẽ, dẫn chứng được đưa ra để chứng minh cho luận điểm trong các phần.
Lời giải chi tiết:
* Phân tích cách sử dụng lí lẽ, bằng chứng của tác giả trong phần 1:
- Luận điểm: Khẳng định độc lập, chủ quyền của dân tộc Đại Việt.
+ Lí lẽ: Đại Việt là một nước văn hiến, có lịch sử lâu đời.
+ Bằng chứng: có nền văn hiến lâu đời, có phong tục tập quán riêng ở mỗi dân tộc, có các triều đại lịch sử Việt Nam và các anh hùng hào kiệt đã bảo vệ đất nước khỏi giặc ngoại xâm.
→ Lí lẽ và bằng chứng đã đi liền với nhau. Bằng chứng được đưa ra cụ thể, ngay kề lí lẽ để làm sáng rõ, góp phần chứng minh cho luận điểm.
* Phân tích cách sử dụng lí lẽ, bằng chứng của tác giả trong phần 2:
- Luận điểm: Tội ác của giặc Minh đi ngược tư tưởng nhân nghĩa không thể tha thứ.
+ Lí lẽ: “Quân cuồng Minh đã thừa cơ gây họa”.
+ Bằng chứng: tác giả đã đưa ra hàng loạt những tội ác của giặc “Nướng dân đen... Tan tác cả nghề canh cửi”.
→ Lí lẽ và bằng chứng đã đi liền với nhau. Bằng chứng được đưa ra cụ thể, ngay kề lí lẽ để làm sáng rõ, góp phần chứng minh cho luận điểm.
Đúng 1
Bình luận (0)
* Cách sử dụng lí lẽ và bằng chứng của tác giả trong phần 1 của bài cáo:
- Lí lẽ: Đại Việt là một nước văn hiến, có lịch sử lâu đời.
- Bằng chứng: Bằng chứng về các triều đại trong lịch sử Việt Nam và các anh hùng hào kiệt đã bảo vệ đất nước khỏi giặc ngoại xâm.
Trong phần 1, lí lẽ và bằng chứng đi liền với nhau. Bằng chứng được nêu ra ngay sau lí lẽ, làm sáng rõ và chứng minh cho lí lẽ.
* Cách sử dụng lí lẽ và bằng chứng của tác giả trong phần 2 của bài cáo:
- Lí lẽ: "Quân cuồng Minh đã thừa cơ gây họa".
- Bằng chứng: "Nướng dân đen... Tan tác cả nghề canh cửi".
Trong phần 2, lí lẽ và bằng chứng cũng đi liền với nhau. Bằng chứng được đưa ra ngay sau lí lẽ, làm sáng rõ và chứng minh cho lí lẽ.
Đúng 0
Bình luận (0)
Giả sử hàm f có đạo hàm cấp n trên R,
n
∈
N
*
và
f
(
1
-
x
)
+
x
2
f
(
x
)
2
x
với mọi
x
∈
ℝ
. Tính tích phân
I
∫
0...
Đọc tiếp
Giả sử hàm f có đạo hàm cấp n trên R, n ∈ N * và f ( 1 - x ) + x 2 f ' ' ( x ) = 2 x với mọi x ∈ ℝ . Tính tích phân I = ∫ 0 1 x f ' ( x ) d x
A. I=1
B. I=-1
C. I= 1 3
D. I= - 1 3
f ( 1 - x ) + x 2 f ' ' ( x ) = 2 x 1
Thay x=0 vào (1) ta được f(1)=0
Đạo hàm hai vế của (1) ta có - f ' ( 1 - x ) + 2 x f ' ' ( x ) + x 2 f ' ' ' ( x ) = 2 2
Thay x=0 vào (2) ta được f'(1)=2
Mặt khác, lấy tích phân hai vế cận từ 0 đến 1 của (1) ta có:
∫ 0 1 f ( 1 - x ) d x + ∫ 0 1 x 2 f ' ' ( x ) d x = ∫ 0 1 2 x d x
⇔ - ∫ 0 1 f ( 1 - x ) d ( 1 - x ) + f ' ( 1 ) - 2 ∫ 0 1 x f ' ( x ) d x = 1 ⇔ ∫ 0 1 f ( x ) d x - 2 ∫ 0 1 x f ' ( x ) d x = 3
Đặt ∫ 1 f ( x ) d x = I 1 . Vì
∫ 0 1 x f ' ( x ) d x = f ( 1 ) - ∫ 0 1 f ( x ) d x = - ∫ 0 1 f ( x ) d x
nên ta có hệ: I 1 - 2 I = 3 I = - I 1 ⇔ I 1 = 1 I = - 1
Vậy I=-1
Chọn đáp án B.
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử (giả sử các biểu thức đều có nghĩa)
1/ x^2 - 3
2/ x-1
3/ a+ căn của a
2). X-1= (√x-1).(√x+1)
3) a+√a= √a (√a+1)
Cac bn nho ung ho mk nha
Đúng 0
Bình luận (0)
Cho số thực a0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a – x) 1,
∀
x
∈
[0;a]. Tính tích phân
I
∫
0
a
1
1
+
f
(
x
)...
Đọc tiếp
Cho số thực a>0. Giả sử hàm số f(x) liên tục và luôn dương trên đoạn [0;a] thỏa mãn f(x).f(a – x) = 1, ∀ x ∈ [0;a]. Tính tích phân I = ∫ 0 a 1 1 + f ( x ) d x
Đáp án A
Phương pháp : Sử dụng phương pháp đổi biến, đặt x = a – t.
Cách giải : Đặt x = a – t => dx = –dt. Đổi cận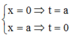 
=> 
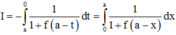
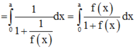
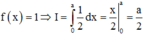
Đúng 0
Bình luận (0)
Các bước trong phương pháp lai và phân tích cơ thể lai của MenĐen gồm: 1. Đưa giả thuyết giải thích kết quả và chứng minh giả thuyết 2. Lai các dòng thuần khác nhau về 1 hoặc vài tính trạng rồi phân tích kết quả ở F1,F2,F3 3. Tạo các dòng thuần chủng 4. Sử dụng toán xác suất để phân tích kết quả lai Trình tự các bước Menđen đã tiến hành nghiên cứu để rút ra được quy luật di truyền là: A. 3, 2, 4, 1. B. 2, 1, 3, 4. C. 1, 2, 3, 4. D. 2, 3, 4, 1.
Đọc tiếp
Các bước trong phương pháp lai và phân tích cơ thể lai của MenĐen gồm:
1. Đưa giả thuyết giải thích kết quả và chứng minh giả thuyết
2. Lai các dòng thuần khác nhau về 1 hoặc vài tính trạng rồi phân tích kết quả ở F1,F2,F3
3. Tạo các dòng thuần chủng
4. Sử dụng toán xác suất để phân tích kết quả lai
Trình tự các bước Menđen đã tiến hành nghiên cứu để rút ra được quy luật di truyền là:
A. 3, 2, 4, 1.
B. 2, 1, 3, 4.
C. 1, 2, 3, 4.
D. 2, 3, 4, 1.
Các bước trong phương pháp lai và phân tích cơ thể lai của MenĐen gồm:1. Đưa giả thuyết giải thích kết quả và chứng minh giả thuyết.2. Lai các dòng thuần khác nhau về 1 hoặc vài tính trạng rồi phân tích kết quả ở F1, F2, F3.3. Tạo các dòng thuần chủng.4. Sử dụng toán xác suất để phân tích kết quả lai.Trình tự các bước Menđen đã tiến hành nghiên cứu để rút ra được quy luật di truyền là: A. 1, 2, 3, 4 B. 2, 3, 4, 1 C. 3, 2, 4, 1 D. 2, 1, 3, 4
Đọc tiếp
Các bước trong phương pháp lai và phân tích cơ thể lai của MenĐen gồm:
1. Đưa giả thuyết giải thích kết quả và chứng minh giả thuyết.
2. Lai các dòng thuần khác nhau về 1 hoặc vài tính trạng rồi phân tích kết quả ở F1, F2, F3.
3. Tạo các dòng thuần chủng.
4. Sử dụng toán xác suất để phân tích kết quả lai.
Trình tự các bước Menđen đã tiến hành nghiên cứu để rút ra được quy luật di truyền là:
A. 1, 2, 3, 4
B. 2, 3, 4, 1
C. 3, 2, 4, 1
D. 2, 1, 3, 4
Giả sử mảng a gồm các phần tử a[1]=1, a[2]=2, a[3]=3, a[4]=4, a[5]=5.
Cho biết kết quả sau khi thực hiện đoạn chương trình sau:
S:=0;
FOR i:=1 to 5 DO
IF a[i] mod 2 = 1 THEN S:=S+a[i];
writeln(‘S = ’,S);
A. 6
B. S = 6
C. 9
D. S = 9
Giả sử mảng a gồm các phần tử a[1]1, a[2]2, a[3]3, a[4]4, a[5]5.Xét đoạn chương trình sau:S : 0; For i :1 to 5 do If a[i] mod 2 1 then S : S+a[i];Write(S);Kết quả hiện ra màn hình là: A. 9 B. S6 C. 6 D. S9
Đọc tiếp
Giả sử mảng a gồm các phần tử a[1]=1, a[2]=2, a[3]=3, a[4]=4, a[5]=5.
Xét đoạn chương trình sau:
S := 0;
For i :=1 to 5 do
If a[i] mod 2 = 1 then S := S+a[i];
Write(S);
Kết quả hiện ra màn hình là:
A. 9
B. S=6
C. 6
D. S=9