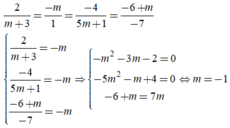Cho hai mặt phẳng P : 2 x + 3 y - z - 1 = 0 , Q : x + 2 y - z + 1 = 0 . Biết d = P ∩ Q . Tìm một vectơ chỉ phương của (d)
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x + 2 y - z - 1 = 0 , (Q): 3x-(m+2)y+(2m-1)z+3=0. Tìm m để hai mặt phẳng (P), (Q) vuông góc với nhau.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x-y+z-1=0 và (Q):2x+y+1=0. Viết phương trình mặt phẳng đi qua A(1;-1;-2) vuông góc với hai mặt phẳng (P) và (Q).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x–y+z -1= 0 và (Q):2x+y+1= 0. Viết phương trình mặt phẳng đi qua A(1;-1;-2) vuông góc với hai mặt phẳng (P) và (Q).
A. x+2y+3z+7=0.
B. x-2y+3z+3=0.
C. x+2y-3z–5=0.
D. x–2y–3z-9=0.
Trong không gian hệ tọa độ Oxyz, cho đường thẳng Δ là giao tuyến của hai mặt phẳng (P): z-1= 0 và (Q): x+y+z-3 =0. Gọi d là đường thẳng nằm trong mặt phẳng (P), cắt đường thẳng: \(\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}\) và vuông góc với đường thẳng Δ. Phương trình đường thẳng d là?
Phương trình \(d_1\) : \(\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}\) dạng tham số: \(\left\{{}\begin{matrix}x=1+t\\t=2-t\\z=3-t\end{matrix}\right.\)
Gọi A là giao điểm d1 và (P), tọa độ A thỏa mãn:
\(3-t-1=0\Rightarrow t=2\Rightarrow A\left(3;0;1\right)\)
\(\overrightarrow{n_P}=\left(0;0;1\right)\) ; \(\overrightarrow{n_Q}=\left(1;1;1\right)\)
\(\overrightarrow{u_{\Delta}}=\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(-1;1;0\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{n_P}\right]=\left(1;1;0\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=3+t\\y=t\\z=1\end{matrix}\right.\)
Trong không gian Oxyz, cho hai mặt phẳng (P): x - 2y - z + 3 = 0,
(Q): 2x + y + z - 1 = 0. Mặt phẳng (R) đi qua điểm M(1;1;1) và chứa
giao tuyến của (P) và (Q).
Phương trình của (R): m.(x - 2y - z + 3) + (2x + y + z -1) = 0. Khi đó giá trị của m là
A. 3
B. 1 3
C. -1
D. -3
Cho hai mặt phẳng ( P ) : ( m - 1 ) x + 2 y – z + 10 = 0 v à ( Q ) : - x + ( 2 m + 1 ) y – m z + 2 = 0 . Tìm m để hai mặt phẳng trên vuông góc với nhau.
A. m = - 3 4
B. m = 3 4
C. m = 4 3
D. m = - 4 3
Chọn A.
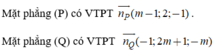
Để hai mặt phẳng đã cho vuông góc với nhau thì
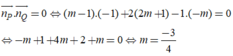
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng P : x+y-z-2=0, Q : x-y+z-1=0
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai mặt phẳng (P): x - 2y - z + 3 =0, (Q): 2x + y + z - 1= 0, . Mặt phẳng R đi qua điểm M(1;1;1) và chứa giao tuyến của (P) và (Q); phương trình của (R): m.(x-2y-z+3) + (2x+y+z-1). Khi đó giá trị của m là
A. 3
B. 1 3
C. - 1 3
D. 3
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng ( P ) : x + y - z - 2 = 0 , ( Q ) : x - y + z - 1 = 0 là
A. x + y + z - 3 = 0
B. x - 2y + z = 0
C. x + z - 2 = 0
D. x + y - 2 = 0
Trong không gian Oxyz, cho hai mặt phẳng ( P ) : 2 x - m y - 4 z - 6 + m = 0 v à ( Q ) : ( m + 3 ) x + y + ( 5 m + 1 ) z - 7 = 0 . Tìm m để hai mặt phẳng (P) và (Q) trùng nhau
A. m = - 6 5
B. m = 1
C. m = -1
D. m = 4
Chọn C.
Để hai mặt phẳng (P) và (Q) trùng nhau khi và chỉ khi: