Chọn A.
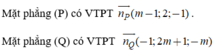
Để hai mặt phẳng đã cho vuông góc với nhau thì
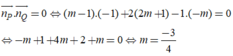
Chọn A.
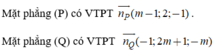
Để hai mặt phẳng đã cho vuông góc với nhau thì
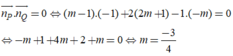
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x + 2 y - z - 1 = 0 , (Q): 3x-(m+2)y+(2m-1)z+3=0. Tìm m để hai mặt phẳng (P), (Q) vuông góc với nhau.
![]()
![]()
![]()
![]()
Trong không gian Oxy cho hai mặt phẳng (P); x-3y+2z+1=0 , (Q): (2m-1)x+m(1-2m)y+ (2m-4)z+14=0. Tìm m để (P) (Q) vuông góc với nhau
A. m ∈ 1 ; - 3 2
B. m ∈ 1 ; 3 2
C. m ∈ - 1 ; - 3 2
D. m ∈ 2
Trong không gian Oxyz, cho hai mặt phẳng ( P ) : 2 x - m y - 4 z - 6 + m = 0 v à ( Q ) : ( m + 3 ) x + y + ( 5 m + 1 ) z - 7 = 0 . Tìm m để hai mặt phẳng (P) và (Q) trùng nhau
A. m = - 6 5
B. m = 1
C. m = -1
D. m = 4
Trong không gian Oxyz, cho ba mặt phẳng (P), (Q), (R) lần lượt có phương trình là ( m 2 + m)x - (m + 2)y + z = 0; x + y + z = 0; 2x + y - z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R)?
A. m = 1
B. m = -1
C. m = -3/2
D. m = -3/2 hoặc m = -1
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0 Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).
Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + my + (m + 3)z + 1 = 0; x - y + 2z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) vuông góc với mặt phẳng (Q)?
A. m = -1
B. m = 0
C. m = -7
D. Không tồn tại m
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với hai mặt phẳng (Q): 2x – y + 3z + 1 = 0 và (R): x – 2y – z + 8 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng P : x + m y + m - 1 z + 2 = 0 , Q : 2 x - y + 3 z - 4 = 0 . Giá trị số thực m để hai mặt phẳng (P); (Q) vuông góc
A. m = 1
B. m = - 1 2
C. m = 2
D. m = 1 2
1.Cho điểm M(1 ; 4 ; 5) và mặt phẳng (α): x + y + z -1 =0. Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).