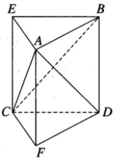
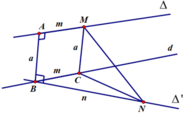
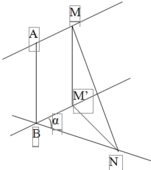
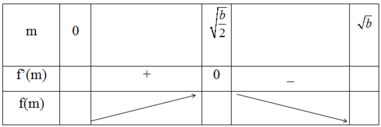
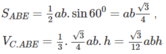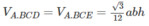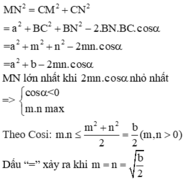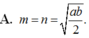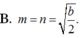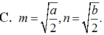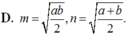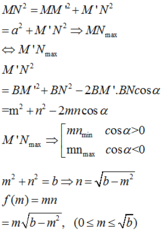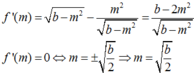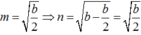AB là đoạn vuông góc chung của 2 đường thẳng ∆ , ∆ ' chéo nhau, A B ∈ ∆ , B ∈ ∆ ' , A B = a M là điểm di động trên ∆ , N là điểm di động trên ∆ ' . Đặt AM=m, AN=n m , n ≥ 0 . Giả sử ta luôn có m 2 + n 2 = b với b>0, b không đổi. Xác định m, n để độ dài đoạn MN đạt giá trị lớn nhất
A. m = n = a b 2
B. m = n = b 2
C. m = a 2 , n = b 2
D. m = a b 2 , n = a + b 2