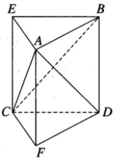
Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC là một lăng trụ đứng.
Ta có:
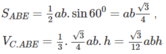
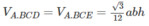

Dựng BE song song và bằng DC, DF song song và bằng BA. Khi đó, ABE.FDC là một lăng trụ đứng.
Ta có:
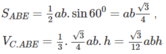
Cho Ax, By là hai nửa đường thẳng chéo nhau vuông góc với nhau. Trên Ax lấy D, By lấy C biết AD = BC, AB là đường vuông góc chung của Ax, By và AB = a, CD = 3a. Tính thể tích V của ABCD.
A. V = a 3 3
B. V = a 3 3 6
C. V = a 3 2 2
D. V = 2 a 3 3
Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d, đoạn thẳng CD có độ dài bằng b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
Cho tứ diện ABCD có A B = C D = 2 3 . Gọi M và N lần lượt là trung điểm các cạnh AC, BD. Biết rằng MN = 3. Số đo góc hợp bởi hai đường thẳng AB, CD bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD biết AB=BC=CA=4, AD=5, CD=6, BD=7. Góc giữa hai đường thẳng AB và CD bằng
A. 60 0 .
B. 120 0 .
C. 30 0 .
D. 150 0 .
Cho tứ diện ABCD có A B = C D = a , A C = B D = b , A D = B C = c . Khoảng cách giữa hai đường thẳng AB và CD là
![]()
![]()
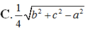
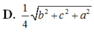
Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng 11 2 . Khi đó độ dài cạnh CD là
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có A B = C D = a , A C = B D = b , A D = B C = c . Gọi α là số đo của góc hợp bởi hai đường thẳng AB, CD. Khi đó cos α bằng

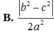
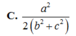
![]()
Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng
![]()
![]()
![]()
![]()
Cho hình trụ có bán kính R và đường cao R√2. Gọi AB và CD là hai đường kính thay đổi của hai đường tròn đáy mà AB vuông góc với CD.
a) Chứng minh rằng ABCD là tứ diện đều.
b) Chứng minh rằng các đường thẳng AC, AD, BC, BD luôn tiếp xúc với một mặt trụ cố định