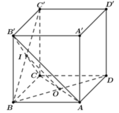
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.
Góc giữa hai đường thẳng A'B và AC' bằng
![]()
![]()
![]()
![]()
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Góc giữa hai đường thẳng A'B và AC' bằng
A. 60 ° .
B. 30 ° .
C. 90 ° .
D. 45 ° .
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a . Tính góc giữa 2 đường thẳng A'B và B'D'
\(BD||B'D'\Rightarrow\widehat{\left(A'B;B'D'\right)}=\widehat{\left(A'B;BD\right)}=\widehat{A'BD}\)
Mặt khác \(A'B=BD=A'D=a\sqrt{2}\) (đều là đường chéo của các hình vuông cạnh a)
\(\Rightarrow\Delta A'BD\) đều \(\Rightarrow\widehat{A'BD}=60^0\)
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, gọi α là góc giữa đường thẳng A ' B và mặt phẳng B B ' D ' D . Tính sin α .
A. 3 5 .
B. 3 2 .
C. 1 2 .
D. 3 4 .
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, gọi α là góc giữa đường thẳng A ' B và mặt phẳng B B ' D ' D . Tính sin α
A. 3 5
B. 3 2
C. 1 2
D. 3 4
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AA' và A'B'. Số đo góc giữa hai đường thẳng MN và BD (như hình vẽ bên) là:
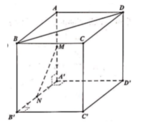
A. 45°.
B. 30°.
C. 60°.
D. 90°.
Chọn đáp án C.
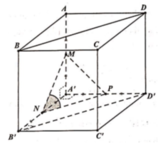
Gọi P là trung điểm cạnh A'D' khi đó BD//NP.
Khi đó góc giữa ![]()
Vì ABCD.A'B'C'D' là hình lập phương cạnh a nên ![]()
Suy ra 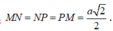
Do đó tam giác MNP đều ![]()
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AA' và A'B'. Số đo góc giữa hai đường thẳng MN và BD (như hình vẽ bên) là:
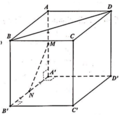
A. 45°.
B. 30°.
C. 60°.
D. 90°.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính góc giữa hai đường thẳng BD và AC
A . 60 0
B . 30 0
C . 45 0
D . 90 0
Đáp án D
Có hình chiếu của AC' xuống đáy là AC mà AC ⊥ BC nên AC'BD.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Góc giữa hai đường thẳng AB' và BC' bằng
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Gọi ![]()
Suy ra OI//AB'. Khi đó ![]()
Ta có ![]()
Suy ra ![]()
![]()
Chọn C.
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai đường thẳng BB ' và AC ' bằng:
![]()
![]()
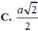
![]()