Cho hình chóp OABC có OA, OB, OC đôi một vuông góc tại O và O A = 2 , O B = 3 , O C = 6. Thể tích của khối chóp bằng
A. 12
B. 6
C. 24
D. 36
Cho hình chóp OABC có OA, OB, OC đôi một vuông góc tại O và OA = 2, OB= 3, OC = 6. Thể tích của khối chóp bằng
A. 12
B. 6
C. 24
D. 36
Cho hình chóp O.ABC có OA, OB, OC đôi một vuông góc tại O và OA=2, OB=3, OC=6. Thể tích của khối chóp bằng:
A. 12
B. 6
C. 24
D. 36.
Cho tứ diện OABC có OA=a; OB=2a; OC=3a đôi một vuông góc với nhau tại O. Lấy M là trung điểm của cạnh AC; N nằm trên cạnh CB sao cho CN=2/3 CB. Tính theo a thể tích khối chóp OAMNB
A. 2 a 3
B. a 3 6
C. 2 a 3 3
D. a 3 3
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và \(OA = a,OB = a\sqrt 2 \) và \(OC = 2a\). Tính khoảng cách từ điểm \(O\) đến mặt phẳng \((ABC)\).
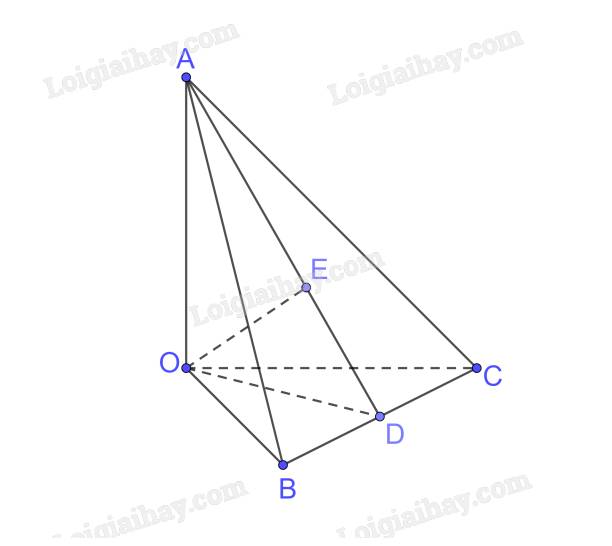
Ta có \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right);BC \subset \left( {OBC} \right) \Rightarrow OA \bot BC\)
Trong (OBC) kẻ \(OD \bot BC\)
\(\begin{array}{l} \Rightarrow BC \bot \left( {OAD} \right);BC \subset \left( {ABC} \right) \Rightarrow \left( {OAD} \right) \bot \left( {ABC} \right)\\\left( {OAD} \right) \cap \left( {ABC} \right) = AD\end{array}\)
Trong (OAD) kẻ \(OE \bot AD\)
\( \Rightarrow OE \bot \left( {ABC} \right) \Rightarrow d\left( {O,\left( {ABC} \right)} \right) = OE\)
Xét tam giác OBC vuông tại O có
\(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow OD = \frac{{2a\sqrt 3 }}{3}\)
Xét tam giác OAD vuông tại O có
\(\frac{1}{{O{E^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{{2a\sqrt 3 }}{3}} \right)}^2}}} = \frac{7}{{4{a^2}}} \Rightarrow OE = \frac{{2a\sqrt 7 }}{7}\)
Vậy \(d\left( {O,\left( {ABC} \right)} \right) = \frac{{2a\sqrt 7 }}{7}\)
cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau tại O và OA=OB=OC=1. Gọi M là trung điểm AB. tính (vecto OM,vecto BC)
Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc. Vẽ đường thẳng qua \(O\) và vuông góc với \(\left( {ABC} \right)\) tại \(H\). Chứng minh \(AH \bot BC\).
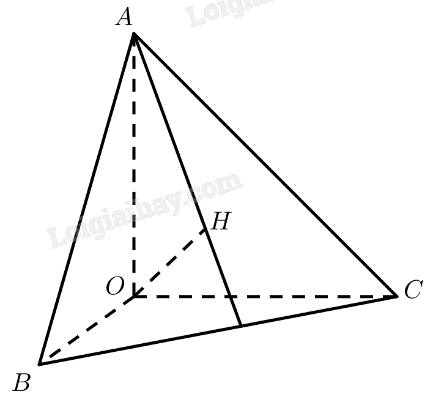
\(\begin{array}{l}\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC\\OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC\\ \Rightarrow BC \bot \left( {OAH} \right) \Rightarrow BC \bot AH\end{array}\)
Cho tứ diện OABC có OA;OB;OC đôi một vuông góc, biết O A = a , O B = 2 a , O C = a 3 Tính khoảng cách từ điểm O đến mặt phẳng (ABC)
A. a 3 2
B. a 9
C. a 17 19
D. 2 a 3 19
Đáp án D
Gọi H là hình chiếu của O xuống (ABC)
Ta có: 1 O H 2 = 1 a 2 + 1 2 a 2 + 1 a 3 2 = 19 12 a 2 ⇒ O H = 2 a 3 19
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc, biết OA =a, OB = 2a, OC = a 3 . Tính khoảng cách từ điểm O đến mặt phẳng (ABC)
A. a 3 2
B. a 9
C. a 17 19
D. 2 a 3 19
Cho tứ diện OABC có OA = a, OB = 2a, OC = 3a đôi vuông góc với nhau tại O. Lấy M là trung điểm của cạnh CA; N nằm trên cạnh CB sao cho C N = 2 3 C B Tính theo a thể tích khối chóp OAMNB
A. 2 a 3
B. 1 6 a 3
C. 2 3 a 3
D. 1 3 a 3