Tìm {M} biểu diễn số phức z thỏa mãn: z + z ¯ - i = 1 .
A. {M} là {(0,0)}
B. {M} là đường tròn x 2 + y - 1 2 = 0
C. {M}là trục tung
D. {M} là đường thẳng x - y = 1
Tìm {M} biểu diễn số phức z thỏa mãn |z-i| = |(1+i)z|.
A. {M} là w: x 2 + y + 1 2 = 2
B. {M} là w: x - 1 2 + y 2 = 1
C. {M} là w: x 2 + y + 1 2 = 1
D. {M} là w: x + 1 2 + y 2 = 2
Cho số phức z thỏa mãn phương trình 3 + 2 i z + z - i 2 = 4 + i . Tìm tọa độ điểm M biểu diễn số phức z.
A. M - 1 ; 1
B. M - 1 ; - 1
C. M 1 ; 1
D. M 1 ; - 1
Cho N là điểm biểu diễn số phức z thỏa mãn \(\dfrac{z+2-3i}{z-3}=1-i\) và M là điểm biểu diễn số phức z' thoả mãn \(\left|z'-2-i\right|+\left|z'+3-3i\right|=\sqrt{29}\). Tìm giá trị nhỏ nhất của MN
Tìm điểm M biểu diễn bởi số phức z thỏa mãn z = (2+3i)(i+1)
A. M(2;3)
B. M(3;4)
C. M(-1;5)
D. M(5;5)
Cho số phức z thỏa mãn (3+i)z = 13 - 9i. Tìm tọa độ của điểm M biểu diễn z.
A. M = (-3;4)
B. M = (3;-4)
C. M = (-3;-4)
D. M = (1;-3)
Đáp án B
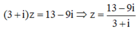
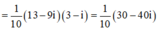
= 3 - 4i
Vậy tọa độ của M(3;-4)
Cho số phức z thỏa mãn ( 3 + i ) z = 13 − 9 i . Tìm tọa độ của điểm M biểu diễn z.
A. M = ( − 3 ; 4 )
B. M = ( 3 ; − 4 )
C. M = ( − 3 ; − 4 )
D. M = ( 1 ; − 3 )
Tìm {M} biểu diễn số phức z thỏa mãn z = |z|
A. {M} là (C): x 2 + y 2 = 1
B. {M}là trục hoành
C. {M} là trục tung
D. {M} = {M(x,0)|x ≥ 0}
Gọi M là điểm biểu diễn số phức z thỏa mãn z = z ¯ . Tìm {M}.
A. {M} = {0(0;0)}
B. {M}là trục Ox.
C. {M}là trục Oy.
D. {M}là (d): y = x.
Tìm {M} biểu diễn số phức z thỏa mãn |z+1|+|z-1| = 4
A. {M} là đường tròn x + 1 2 + y - 1 2 = 4
B. {M} là {(-2;0),(2;0)}
C. {M} là đường thẳng x+y-4 = 0
D. {M} là Elip x 2 4 + y 2 3 = 1