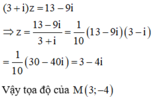Các câu hỏi tương tự
Cho số phức z thỏa mãn phương trình
3
+
2
i
z
+
z
-
i
2
4
+
i
. Tìm tọa độ điểm M biểu diễn số phức z. A.
M
-
1
;
1
...
Đọc tiếp
Cho số phức z thỏa mãn phương trình 3 + 2 i z + z - i 2 = 4 + i . Tìm tọa độ điểm M biểu diễn số phức z.
A. M - 1 ; 1
B. M - 1 ; - 1
C. M 1 ; 1
D. M 1 ; - 1
Cho số thực a thay đổi và số phức z thỏa mãn
z
a
2
+
1
i
-
a
1
-
a
a
-
2
i
.
Trên mặt phẳng tọa độ,...
Đọc tiếp
Cho số thực a thay đổi và số phức z thỏa mãn z a 2 + 1 = i - a 1 - a a - 2 i . Trên mặt phẳng tọa độ, gọi M là điểm biểu diễn số phức z . Khoảng cách giữa hai điểm M và I (-3; 4) (khi a thay đổi) là:
A. 4
B. 3
C. 5
D. 6
Tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện
z
+
z
+
3
4
là A. Đường thẳng
x
1
2
B. Đường thẳng
x
-
7
2
C. Hai đường thẳng
x
1...
Đọc tiếp
Tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện z + z + 3 = 4 là
A. Đường thẳng x = 1 2
B. Đường thẳng x = - 7 2
C. Hai đường thẳng x = 1 2 và x = 7 2
D. Hai đường thẳng x = 1 2 và x = - 7 2
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
z
z
-
i
3
A. Đường tròn tâm
I
9
8
;
0
bán kính
R
3
8
B. Đường tr...
Đọc tiếp
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z z - i = 3
A. Đường tròn tâm I 9 8 ; 0 bán kính R = 3 8
B. Đường tròn tâm I 0 ; 9 8 bán kính R = 9 64
C. Đường tròn tâm I 0 ; 9 8 bán kính R = 3 8
D. Đường tròn tâm I 0 ; - 9 8 bán kính R = 9 64
Cho số phức z thỏa mãn:
z
1
+
2
i
-
z
¯
2
-
3
i
-
4
+
12
i
. Tìm tọa độ điểm M biểu diễn số phức z. A.
M
3
;
1...
Đọc tiếp
Cho số phức z thỏa mãn: z 1 + 2 i - z ¯ 2 - 3 i = - 4 + 12 i . Tìm tọa độ điểm M biểu diễn số phức z.
A. M 3 ; 1
B. M 3 ; - 1
C. M - 1 ; 3
D. M 1 ; 3
Cho số phức z thỏa mãn (2 - i)z = (2 + i)(1 - 3i). Gọi M là điểm biểu diễn của z. Khi đó tọa độ điểm M là.
A. M(3;1)
B. M(3;-1)
C. M(1;3)
D. M(1;-3)
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
1
z
3
A. Phần hình phẳng nằm hoàn toàn phía ngoài hình tròn (O,1) và phía trong hình tròn (O,3) B. Hình tròn (O,3) (bỏ gốc tọa độ O) C. Hình tròn (O,1) (bỏ gốc tọa độ O) D. Đường tròn (O,1)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn 1 < z < 3
A. Phần hình phẳng nằm hoàn toàn phía ngoài hình tròn (O,1) và phía trong hình tròn (O,3)
B. Hình tròn (O,3) (bỏ gốc tọa độ O)
C. Hình tròn (O,1) (bỏ gốc tọa độ O)
D. Đường tròn (O,1)
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
z
-
3
-
4
i
2
A. Đường tròn tâm I(3;4) bán kính
R
2
B. Đường tròn tâm I(3;4) bán kính R2 C. Đường tròn tâm I(3;-4) bán kính
R...
Đọc tiếp
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z - 3 - 4 i = 2
A. Đường tròn tâm I(3;4) bán kính R = 2
B. Đường tròn tâm I(3;4) bán kính R=2
C. Đường tròn tâm I(3;-4) bán kính R = 2
D. Đường tròn tâm I(3;-4) bán kính R=2
Trên mặt phẳng tọa độ Oxyz, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
z
z
-
3
+
4
i
là đường thẳng A.
2
x
-
3
0
B.
6
x
-
8
y
-
25...
Đọc tiếp
Trên mặt phẳng tọa độ Oxyz, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z = z - 3 + 4 i là đường thẳng
A. 2 x - 3 = 0
B. 6 x - 8 y - 25 = 0
C. 6 x + 8 y - 25 = 0
D. y - 2 = 0