Các câu hỏi tương tự
Cho các số phức z thỏa mãn
z
-
i
z
-
1
+
2
i
. Tập hợp các điểm biểu diễn số phức
w
(
2
-
i
)
z
+
1
trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là A.
x
-
7
y
-
9
0...
Đọc tiếp
Cho các số phức z thỏa mãn z - i = z - 1 + 2 i . Tập hợp các điểm biểu diễn số phức w = ( 2 - i ) z + 1 trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. x - 7 y - 9 = 0
B. x + 7 y - 9 = 0
C. x + 7 y + 9 = 0
D. x - 7 y + 9 = 0
Cho số phức z thay đổi hoàn toàn thỏa mãn:
z
−
i
z
−
1
+
2
i
. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn:
w
2
−...
Đọc tiếp
Cho số phức z thay đổi hoàn toàn thỏa mãn: z − i = z − 1 + 2 i . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = 2 − i z + 1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. − x + 7 y + 9 = 0.
B. x + 7 y − 9 = 0.
C. x + 7 y + 9 = 0.
D. x − 7 y + 9 = 0.
Cho các số phức z thỏa mãn |z+1-i|=|z-1+2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó
A. 4x+6y-3= 0
B. 4x-6y-3=0
C. 4x+6y+3=0
D. 4x-6y+3=0
Cho số phức
z
a
+
b
i
;
a
,
b
∈
ℝ
Để điểm biểu diễn của z trên mặt phẳng tọa độ thuộc dải giới hạn bởi hai đường thẳng x -3 và x 3 như hình vẽ bên thì điều kiện của a và b là: A.
a
≤
-
3...
Đọc tiếp
Cho số phức z = a + b i ; a , b ∈ ℝ Để điểm biểu diễn của z trên mặt phẳng tọa độ thuộc dải giới hạn bởi hai đường thẳng x = -3 và x = 3 như hình vẽ bên thì điều kiện của a và b là:
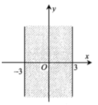
A. a ≤ - 3 b ≤ - 3
B. a ≤ 3 b ≥ - 3
C. a ≥ 3 b ≥ 3
D. - 3 ≤ a ≤ 3 b ∈ ℝ
Trên mặt phẳng tọa độ Oxyz, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn
z
z
-
3
+
4
i
là đường thẳng A.
2
x
-
3
0
B.
6
x
-
8
y
-
25...
Đọc tiếp
Trên mặt phẳng tọa độ Oxyz, tìm tập hợp các điểm M biểu diễn số phức z thỏa mãn z = z - 3 + 4 i là đường thẳng
A. 2 x - 3 = 0
B. 6 x - 8 y - 25 = 0
C. 6 x + 8 y - 25 = 0
D. y - 2 = 0
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.
Trong không gian Oxyz, cho điểm
A
1
;
2
;
-
1
, đường thẳng d:
x
-
1
2
y
+
1
1
z
-
2
-...
Đọc tiếp
Trong không gian Oxyz, cho điểm A 1 ; 2 ; - 1 , đường thẳng d: x - 1 2 = y + 1 1 = z - 2 - 1 và mặt phẳng (P): x + y + 2 z + 1 = 0 . Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là
A. 3 ; - 2 ; - 1
B. - 3 ; 8 ; - 3
C. 0 ; 3 ; - 2
D. 6 ; - 7 ; 0
Trên mặt phẳng phức, tập hợp các số phức
z
x
+
y
i
x
,
y
∈
ℝ
thỏa mãn
z
+
2
+
i
z
¯
-
3
i...
Đọc tiếp
Trên mặt phẳng phức, tập hợp các số phức z = x + y i x , y ∈ ℝ thỏa mãn z + 2 + i = z ¯ - 3 i là đường thẳng có phương trình
A. y = x + 1
B. y = - x + 1
C. y = - x - 1
D. y = x - 1
Cho số phức za+bi, a,bÎR. Điểm biểu diễn của z trên mặt phẳng tọa độ thuộc dải giới hạn bởi hai đường thẳng y -2 và y 2 như hình vẽ bên thì điều kiện của a và b là: A.
-
2
≤
a
≤
2
b
∈
R
B. ...
Đọc tiếp
Cho số phức z=a+bi, a,bÎR. Điểm biểu diễn của z trên mặt phẳng tọa độ thuộc dải giới hạn bởi hai đường thẳng y = -2 và y = 2 như hình vẽ bên thì điều kiện của a và b là:
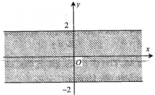
A. - 2 ≤ a ≤ 2 b ∈ R
B. a ≤ 2 b ≥ - 2
C. - 2 ≤ a ≤ 2 - 2 ≤ b ≤ 2
D. a ∈ R - 2 ≤ b ≤ 2




