Cho tích phân I = ∫ 0 1 3 x + 2 ln ( 3 x + 1 ) x + 1 2 d x = ∫ 0 1 a 3 x + 1 - b x + 1 d x - 3 2 + ln 2 . Tính A = a 2 - b 4 . Chọn đáp án đúng:
A. 0
B. 2
C. 3
D. 4
Những câu hỏi liên quan
Cho hàm số yf(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx1, x ϵ [0;π/3] và f(0)1. Tính tích phân
I
∫
0
π
3
f
x
d
x
A. 1/2 + π/3 B.
3
+
1
2
C. ...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Cho hàm số
y
f
x
x
2
k
h
i
...
Đọc tiếp
Cho hàm số y = f x = x 2 k h i 0 ≤ x ≤ 2 - x k h i 1 ≤ x ≤
Tính tích phân I = ∫ 0 2 f x d x
A. 5 6
B. 1 3
C. 2
D. 3
Cho hàm số
y
f
(
x
)
x
2
k
h
i
0
≤
x
≤
1
2...
Đọc tiếp
Cho hàm số y = f ( x ) = x 2 k h i 0 ≤ x ≤ 1 2 - x k h i 1 ≤ x ≤ 2
Tính tích phân I= ∫ 0 2 f ( x ) d x
Cho hàm số f(x) thỏa mãn
∫
0
1
(
x
+
1
)
f
(
x
)
d
x
10
và 2f(1) - f(0) 2 .Tính tích phân
I
∫
0
1
f
(
x
)
d
x
.
A. I-12. B. I8. C. I12. D. I-8
Đọc tiếp
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) - f(0) = 2 .Tính tích phân I = ∫ 0 1 f ( x ) d x .
A. I=-12.
B. I=8.
C. I=12.
D. I=-8
Cho hàm số y f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) 1 và
I
∫
0
1
f
x
d
x
2
. Tính tích phân
I
∫
0
1
f
x
d
x
A. I -1. B. I 1. C. I 2. D. I -2.
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) = 1 và I = ∫ 0 1 f x d x = 2 . Tính tích phân I = ∫ 0 1 f ' x d x
A. I = -1.
B. I = 1.
C. I = 2.
D. I = -2.
Chọn D.
Xét I = ∫ 0 1 f ' x d x Đặt t = x → t 2 = x → 2 t d t = d x
Đổi cận x = 0 → t = 0 x = 1 → t = 1 . Khi đó I = 2 ∫ 0 1 t f ' ( t ) d t = 2 A
Tính A = ∫ 0 1 t f ' ( t ) d t . Đặt u = t d v = f ' t d t → d u = d t v = f t
Khi đó
Đúng 0
Bình luận (0)
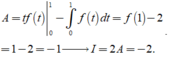
Tính tích phân : \(I=\int\limits_{\frac{-1}{2}}^0\frac{dx}{\left(x+1\right)\sqrt{3+2x-x^2}}\)
\(I=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)\sqrt{3+2x-x^2}}=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)\left(\sqrt{\left(x+1\right)\left(3-x\right)}\right)}\)
\(=\int\limits^0_{\frac{-1}{2}}\frac{dx}{\left(x+1\right)^2\sqrt{\frac{3-x}{x+1}}}\)
Đặt \(t=\sqrt{\frac{3-x}{x+1}}\Rightarrow\frac{dx}{\left(x+1\right)^2}=-\frac{1}{2}\)
Đổi cận : \(x=-\frac{1}{2}\Rightarrow t=\sqrt{7};x=0\Rightarrow t=\sqrt{3}\)
\(I=-\frac{1}{2}\int\limits^{\sqrt{3}}_{\sqrt{7}}dt=\frac{1}{2}\left(\sqrt{7}-\sqrt{3}\right)\)
Đúng 0
Bình luận (0)
Một học sinh làm bài tích phân
I
∫
0
1
d
x
1
+
x
2
theo các bước sauBước 1: Đặt
x
tan
t
,
suy ra
d
x
1
+
tan...
Đọc tiếp
Một học sinh làm bài tích phân I = ∫ 0 1 d x 1 + x 2 theo các bước sau
Bước 1: Đặt x = tan t , suy ra d x = 1 + tan 2 t d t
Bước 2: Đổi x = 1 ⇒ t = π 4 , x = 0 ⇒ t = 0
Bước 3: I = ∫ 0 π 4 1 + tan 2 t 1 + tan 2 t d t = ∫ 0 π 4 d t = t 0 π 4 = 0 − π 4 = − π 4
Các bước làm trên, bước nào bị sai
A. Bước 3
B. Bước 2
C. Không bước nào sai cả
D. Bước 1
Phân tích thành nhân tử
(x-3)^2-5(x-2)+5=0
(2x-1)^2-3(x-2)(x+2)-25=0
\(\left(x-3\right)^2-5\left(x-2\right)+5=0\\ \Leftrightarrow x^2-6x+9-5x+10+5=0\\ \Leftrightarrow x^2-11x+24=0\\ \Leftrightarrow\left(x-8\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
\(\left(2x-1\right)^2-3\left(x-2\right)\left(x+2\right)-25=0\\ \Leftrightarrow4x^2-4x+1-3\left(x^2-4\right)-25=0\\ \Leftrightarrow4x^2-4x-24-3x^2+12=0\\ \Leftrightarrow x^2-4x-12=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a: Ta có: \(\left(x-3\right)^2-5\left(x-2\right)+5=0\)
\(\Leftrightarrow x^2-6x+9-5x+10+5=0\)
\(\Leftrightarrow x^2-11x+24=0\)
\(\Leftrightarrow\left(x-8\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
b: Ta có: \(\left(2x-1\right)^2-3\left(x-2\right)\left(x+2\right)-25=0\)
\(\Leftrightarrow4x^2-4x+1-3x^2+12-25=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hàm số y f(x), y g(x) là các hàm số có đạo hàm và liên tục trên [0; 2] và
∫
0
2
g
x
f
x
d
x
2
,
∫
0
2
g
x
f
x...
Đọc tiếp
Cho hàm số y = f(x), y = g(x) là các hàm số có đạo hàm và liên tục trên [0; 2] và ∫ 0 2 g x f ' x d x = 2 , ∫ 0 2 g ' x f x d x = 3 . Tính tích phân I = ∫ 0 2 [ g x f x ] ' d x .
A. I = –1
. I = 1
C. I = 5
D. I = 6
1 /Phân tích đa thức thành nhân tử :
x3-19x-30
2/Cho a+b+c=0. Chứng minh (a2+b2+c2) = 2(a4+b4+c4).
1. x^3-19x-30
=x^3-25x+6x-30
=x(x^2-25)+6(x-5)
=x(x+5)(x-5)+6(x-5)
=(x-5)(x^2+5x+6)
=(x-5)(x^2+2x+3x+6)
=(x-5)[x(x+2)+3(x+2)]
=(x-5)(x+2)(x+3)
Đúng 0
Bình luận (1)
2.
a + b + c = 0
<=> (a + b + c)² = 0
<=> a² + b² + c² + 2(ab + bc + ca) = 0
<=> a² + b² + c² = -2(ab + bc + ca) ------------(1)
CẦn chứng minh:
2(a^4 + b^4 + c^4) = (a² + b² + c²)²
<=> 2(a^4 + b^4 + c^4) = a^4 + b^4 + c^4 + 2(a²b² + b²c² + c²a²)
<=> a^4 + b^4 + c^4 = 2(a²b² + b²c² + c²a²)
<=> (a² + b² + c²)² = 4(a²b² + b²c² + c²a²) ---(cộng 2 vế cho 2(a²b² + b²c² + c²a²) )
<=> [-2(ab + bc + ca)]² = 4(a²b² + b²c² + c²a²) ----(do (1))
<=> 4.(a²b² + b²c² + c²a²) + 8.(ab²c + bc²a + a²bc) = 4(a²b² + b²c² + c²a²)
<=> 8.(ab²c + bc²a + a²bc) = 0
<=> 8abc.(a + b + c) = 0
<=> 0 = 0 (đúng), Vì a + b + c = 0
=> Đpcm
Đúng 0
Bình luận (1)
bài 1)
\(x^3-19x-30=x^3+2x^2-2x^2-4x-15x-30\)
=\(x^2\left(x+2\right)-2x\left(x+2\right)-15\left(x+2\right)\)
=\(\left(x+2\right)\left(x^2-2x-15\right)\)
=\(\left(x+2\right)\left(x+3\right)\left(x-5\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời