Hình chóp SABCD có đáy ABCD là hình chữ nhật. S A ⊥ A B C D Biết S A = a , B C = a 3 , C D = 2 a . Tính bán kính R của mặt cầu ngoại tiếp SABCD
![]()
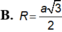
![]()
![]()
Cho hình chóp SABCD có đáy là hình chữ nhật, AB=2a, BC=a. Hình chiếu vuông góc của S trên (ABCD) là trung điểm H của AD, S H = a 3 2 . Tính diện tích mặt cầu ngoại tiếp hình chóp SABCD
A. 4 πa 2 3
B. 16 πa 2 3
C. 16 πa 2 3
D. 4 πa 3 3
Cho hình chóp SABCD đáy ABCD là hình chữ nhật tâm I ,AB =a, BC=a căn 3 .Tam giác SIA cân tại S . (SAD) vuông góc với đáy .góc giữa SD và (ABCD) = 60* .Tính thể tích khối chóp SABCI?
Cho hình chóp SABCD đáy ABCD là hình chữ nhật: AB= 2a, AD = a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB;SC tạo với đáy góc 45 ° . Khoảng cách từ A đến mặt phẳng (SCD) là
A. a 3 3 .
B. a 6 4 .
C. a 6 3 .
D. a 6 6 .
Đáp án C

Gọi M là trung điểm của CD. Kẻ HK vuông góc với SM.
Ta có: C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ ( S H M ) ⇒ ⊥ H K
Mặt khác ta có H K ⊥ S M
Suy ra H K ⊥ ( S C D )
Vậy d ( A , ( S C D ) ) = D ( H , ( S C D ) ) = H K
Xét tam giác BHC vuông tại B, ta có:
H C = B H 2 + B C 2 = a 2 ⇒ S H = H C = a 2
Xét tam giác SHM vuông tại H, ta có:
1 H K 2 = 1 S H 2 + 1 M H 2 = 1 2 a 2 + 1 a 2 = 3 2 a 2 ⇒ H K = a 6 3
Cho hình chóp SABCD đáy ABCD là hình chữ nhật: AB=2a, AD= a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB;SC tạo với đáy góc 45 ° . Khoảng cách từ A đến mặt phẳng (SCD) là
A. a 3 3 .
B. a 6 4 .
C. a 6 4 .
D. a 6 6 .
Đáp án C
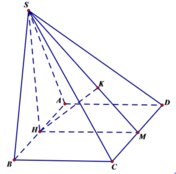
Gọi M là trung điểm của CD. Kẻ HK vuông góc với SM.
Ta có: C D ⊥ H M C D ⊥ S H ⇒ C D ⊥ ( S H M ) ⇒ ⊥ H K
Mặt khác ta có H K ⊥ ( S C D )
Suy ra H K ⊥ ( S C D )
Vậy d ( A , ( S C D ) ) = D ( H , ( S C D ) ) = H K
Xét tam giác BHC vuông tại B, ta có:
H C = B H 2 + B C 2 = a 2 ⇒ S H = H C = a 2
Xét tam giác SHM vuông tại H, ta có:
1 H K 2 = 1 S H 2 + 1 M H 2 = 1 2 a 2 + 1 a 2 = 3 2 a 2 ⇒ H K = a 6 3
Hình chóp SABCD có đáy ABCD là hình chữ nhật có AD = 2a. SA = SB = a;
(SAD) ⊥ (ABCD). Tính thể tích V của hình chóp.
A. V = a 3 6 6
B. V = a 3 3 6
C. V = 2 a 3 3
D. V = a 3 3 3
Hình chóp SABCD, đáy ABCD là hình thoi, ∆ BCD là ∆ đều cạnh a, tâm H. Biết SH ⊥ (ABCD) và ∆ SAC vuông tại S. Tính thể tích V của SABCD.
A. V = a 3 3 4
B. V = a 3 2 6
C. V = a 3 3 3
D. V = a 3 3
Hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, SA ⊥ (ABCD) tạo với mặt đáy một góc 45 0 . Mặt cầu ngoại tiếp hình chóp S. ABCD có bán kính bằng a 2 . Thể tích khối chóp S. ABCD bằng:
![]()
![]()
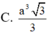
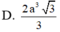
Chọn đáp án D
Gọi O là tâm của hình chữ nhật ABCD và I là trung điểm của SC. Khi đó OI ⊥ (ABCD)
⇒ IA = IB = IC = ID với ∆ S A C vuông tại A, IA = IS = IC. Do đó I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD suy ra IA = a 2 ⇒ SC = 2a 2 . Mặt khác AC là hình chiếu của SC trên mặt phẳng (ABCD).
![]()
Suy ra ∆ S A C vuông cân
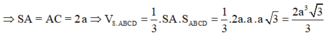
Cho hình chóp SABCD có đáy là hình chữ nhật tâm I, H là trung điểm của AI và SH vuông góc với đáy. Tính \(d_{\left(C,\left(SBD\right)\right)}\) biết \(AB=a,BC=a\sqrt{3}\) và tam giác SAC vuông tại S.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật cạnh a, S A ⊥ (A B C D) ,SC tạo với mặt đáy một góc 60 độ và (SAB ) một góc a với sin a = căn 3/ 4 . Tính chiều cao khối chóp.
Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?