Tìm tập hợp tất cả các giá trị của tham số m để hàm số y = e - 1 3 x 3 + x 2 + m x nghịch biến trên khoảng ( 0 ; + ∞ )
A. m ≤ - 1
B. m < - 1
C. m ≥ - 1
D. m > - 1
Tìm tập hợp tất cả các giá trị của tham số m để hàm số y = x 2 + 3 - m ( x + 1 ) đồng biến trên khoảng ( - ∞ ; + ∞ )
A. [ 1 ; + ∞ )
B. [ - 1 ; 1 ]
C. ( - ∞ ; - 1 ]
D. ( - ∞ ; 1 )
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = | x | 3 - ( 2 m + 1 ) x 2 + 3 m | x | - 5 có 3 điểm cực trị.
A. - ∞ ; 1 4
B. 1 ; + ∞
C. ( - ∞ ; 0 ]
D. 0 ; 1 4 ∪ 1 ; + ∞
Cho hàm số y = 2 x 3 - 3 m x 2 + 3 ( 5 m 2 + 1 ) x - 3 s i n x với m là tham số thực. Tìm tập hợp tất cả các giá trị của m để hàm số đồng biến trên (l;3).
A . m ≥ 1
B . m ≤ - 1
C . m > 0
D . m ∈ R
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m 2 + 2 m ) x - 3 nghịch biến trên khoảng ( 0 ; 1 )
A. [ - 1 ; + ∞ )
B. ( - ∞ ; 0 ]
C. [ - 1 ; 0 ]
D. [ 0 ; 1 ]
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = ln x 2 + 1 - m x + 1 đồng biến trên khoảng ( -∞; +∞).
A. ( - ∞ ; - 1 ]
B. ( - ∞ ; - 1 )
C. - 1 ; 1
D. Đáp án khác
Chọn A.
Ta có: y ' = 2 x x 2 + 1 - m
Hàm số y = ln x 2 + 1 - m x + 1 đồng biến trên khoảng( -∞; +∞). Khi và chỉ khi y’ ≥0 với mọi . ⇔ g ( x ) = 2 x x 2 + 1 ≥ m , ∀ x ∈ - ∞ ; + ∞
Ta có 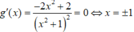
Bảng biến thiên:
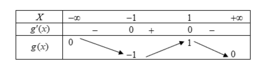
Dựa vào bảng biến thiên ta có:
![]()
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = x 2 + 1 - m x - 1 đồng biến trên khoảng ( - ∞ ; + ∞ ) .
A. - ∞ ; 1
B. [ 1 ; + ∞ )
C. - 1 ; 1
D. - ∞ ; - 1
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = x 2 + 1 − mx − 1 đồng biến trên khoảng − ∞ ; + ∞ ?
A. − ∞ ; 1 .
B. 1 ; + ∞ .
C. − 1 ; 1 .
D. − ∞ ; − 1 .
Đáp án D
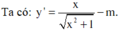
Để hàm số đã cho đồng biến trên khoảng − ∞ ; + ∞ thì y ' > 0 , ∀ x ∈ ℝ
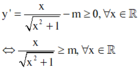
Xét hàm số y = x x 2 + 1 có y ' = 1 x 2 + 1 x 2 + 1 > 0 , ∀ x ∈ ℝ => Hàm số y' luôn đồng biến.
Ta có: lim x → − ∞ x x 2 + 1 = − 1
Vậy để hàm số đã cho đồng biến trên khoảng − ∞ ; + ∞ thì m ≤ − 1 .
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = ln x 2 + 1 − m x + 1 đồng biến trên khoảng − ∞ ; + ∞
A. − ∞ ; − 1
B. − 1 ; 1
C. − 1 ; 1
D. − ∞ ; − 1
Đáp án D
y ' = 2 x x 2 + 1 − m = 2 x − m x 2 + 1 x 2 + 1 T H 1 : m = 0 ⇔ 2 x x 2 + 1 > 0 ⇔ x > 0 T H 2 : m ≠ 0
Hàm số đồng biến trên khoảng
− ∞ ; + ∞ ⇔ − m x 2 + 2 x − m > 0 ∀ x ∈ ℝ
⇔ − m > 0 Δ ' = 1 − m 2 ≤ 0 ⇔ m < 0 m ≥ 1 m ≤ − 1 ⇔ m ≤ − 1
Tìm tập hợp tất cả các giá trị của tham số m để hàm số y = 1 3 x 3 + 2 x 2 - 2 m - 3 x + 4 đồng biến trên - 1 ; + ∞ .
![]()
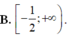
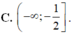
![]()