Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, OO’ = 3cm. Qua A kẻ một đường thẳng cắt các đường tròn (O) và (O’) theo thứ tự tại E và F (A nằm giữa E và F). Tính xem đoạn thẳng EF có độ dài lớn nhất bằng bao nhiêu?

Những câu hỏi liên quan
Cho hai đường tròn (O) và (O') cắt nhau tại A và B, OO' = 3cm. Qua A kẻ một đường thẳng cắt các đường tròn (O) và (O') theo thứ tự tại E và F (A nằm giữa E và F). Tính xem đoạn thẳng EF có độ dài lớn nhất bằng bao nhiêu ?
Cho đoạn thẳng OO bằng 2cm.a. Vẽ đường tròn tâm O bán kính 1,5cm, đường tròn này cắt đoạn thẳng OO tại C và cắt đường thẳng OO ở D.b. Vẽ đường tròn tâm O bán kính bằng 1cm, đường tròn này cắt đoạn thẳng OO tại E và cắt đường thẳng OO tại F. Hai đường tròn trên cắt nhau ở A và B.c. Hãy kể tên đường kính của đường tròn (O’; 1cm) và đường kính của đường tròn (O; 1,5cm) và các dây cung của hai đường tròn trên, rồi tính các đường kính đó.d. Hãy chứng tỏ E là trung điểm của OO.e. Tính độ dài đoạn thẳn...
Đọc tiếp
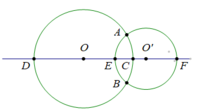
Cho đoạn thẳng OO' bằng 2cm.
a. Vẽ đường tròn tâm O bán kính 1,5cm, đường tròn này cắt đoạn thẳng OO' tại C và cắt đường thẳng OO' ở D.
b. Vẽ đường tròn tâm O' bán kính bằng 1cm, đường tròn này cắt đoạn thẳng OO' tại E và cắt đường thẳng OO' tại F. Hai đường tròn trên cắt nhau ở A và B.
c. Hãy kể tên đường kính của đường tròn (O’; 1cm) và đường kính của đường tròn (O; 1,5cm) và các dây cung của hai đường tròn trên, rồi tính các đường kính đó.
d. Hãy chứng tỏ E là trung điểm của OO'.
e. Tính độ dài đoạn thẳng DF.
a. b.
c. - Đường tròn (O’; 1cm) có đường kính là: EF; Các dây cung là: EA, EB, AB, FA, FB
Vì E thuộc (O’; 1cm) nên EO’=1cm; EF=2.EO’=2cm
- Đường tròn (O; 1,5cm) có đường kính là: DC; Các dây cung là: DA, DB, AB, AC, CB
Vì C thuộc (O; 1,5cm) nên CO=1,5cm; DC=2.CO=3cm
d. Vì đường tròn (O’; 1cm) cắt đoạn thẳng OO’ tại E, nên E nằm giữa 2 điểm O và O’.
Ta có: O E + E O ' = O O ' ⇒ O E = 1 c m
Mà EO’=1cm, nên OE=EO’ (=1cm)
Do đó: E là trung điểm của đợn thẳng OO’.
e. Vì đường tròn (O; 1cm) cắt đường thẳng OO’ tại D, đường tròn (O’; 1cm) cắt đường thẳng OO’ tại F, nên 4 điểm D, O, O’, F lần lượt theo thứ tự đó và DO=1,5cm; O’F=1cm.
Ta có: D F = D O + O O ' + O ' F = 1 , 5 + 2 + 1 = 4 , 5 c m .
Vậy DF=4,5cm
Đúng 0
Bình luận (1)
Cho hai đường tròn (O) và )(O) cắt nhau tại A và B. Vẽ AC,AD thứ tự là đường kính của hai đường tròn (O) và (O)a) Cm C,B,D thẳng hàngb) Đường thẳng AC cắt (O) tại E, AD cắt (O) tại F (E,F khác A). Chứng minh 4 điểm C,D,E,F cùng thuộc 1 đường trònc) Một đường thẳng d thay đổi luôn đi qua A cắt (O) và (O) thứ tự tại M và N . Xác định trí của d để CM+DN đạt giá trị lớn nhất
Đọc tiếp
Cho hai đường tròn (O) và )(O') cắt nhau tại A và B. Vẽ AC,AD thứ tự là đường kính của hai đường tròn (O) và (O')
a) Cm C,B,D thẳng hàng
b) Đường thẳng AC cắt (O') tại E, AD cắt (O) tại F (E,F khác A). Chứng minh 4 điểm C,D,E,F cùng thuộc 1 đường tròn
c) Một đường thẳng d thay đổi luôn đi qua A cắt (O) và (O') thứ tự tại M và N . Xác định trí của d để CM+DN đạt giá trị lớn nhất
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Trên tia đối của tia AB lấy điểm M. Qua M kẻ đường thẳng (d) cắt (O) tại C và D (C nằm giữa M và D), đường thẳng (d') cắt (O') tại E và F (E nằm giữa F và M). Chứng minh CDFE là tứ giác nội tiếp
Xét tứ giác ACDB có A,C,D,B cùng nằm trên (O)
nên ACDB là tứ giác nội tiếp
=>\(\widehat{CAB}+\widehat{CDB}=180^0\)
mà \(\widehat{CAB}+\widehat{MAC}=180^0\)(hai góc kề bù)
nên \(\widehat{MAC}=\widehat{CDB}=\widehat{MDB}\)
Xét tứ giác AEFB có A,E,F,B cùng nằm trên (O')
nên AEFB là tứ giác nội tiếp
=>\(\widehat{BAE}+\widehat{BFE}=180^0\)
mà \(\widehat{BAE}+\widehat{MAE}=180^0\)(hai góc kề bù)
nên \(\widehat{MAE}=\widehat{MFB}\)
Xét ΔMCA và ΔMBD có
\(\widehat{MAC}=\widehat{MDB}\)
\(\widehat{M}\) chung
Do đó: ΔMCA đồng dạng với ΔMBD
=>\(\dfrac{MC}{MB}=\dfrac{MA}{MD}\)
=>\(MC\cdot MD=MA\cdot MB\)(1)
Xét ΔMAE và ΔMFB có
\(\widehat{MAE}=\widehat{MFB}\)
\(\widehat{M}\) chung
Do đó: ΔMAE đồng dạng với ΔMFB
=>\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=>\(MA\cdot MB=MF\cdot ME\left(2\right)\)
Từ (1) và (2) suy ra \(MC\cdot MD=ME\cdot MF\)
=>\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
Xét ΔMCE và ΔMFD có
\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
\(\widehat{CME}\) chung
Do đó: ΔMCE đồng dạng với ΔMFD
=>\(\widehat{MCE}=\widehat{MFD}\)
mà \(\widehat{MCE}+\widehat{DCE}=180^0\)(hai góc kề bù)
nên \(\widehat{MFD}+\widehat{DCE}=180^0\)
=>CDFE là tứ giác nội tiếp
Đúng 2
Bình luận (0)
Từ điểm A ở ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến (O) với B, C là các tiếp điểm. Kẻ một đường thẳng d nằm giữa hai tia AB, AO và đi qua A cắt đường tròn (O) tại E, F (E nằm giữa A, F).1. Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.2. Gọi H là giao điểm của AD và BC. Chứng minh OH.OA OE^2.3. Đường thẳng qua O vuông góc với EF cắt BC tại E. Chứng minh SF là tiếp tuyến của đường tròn (O).4. Đường thẳng SF cắt các đường thẳng AB và AC tương ứng tại P và Q. Đường thẳng OF c...
Đọc tiếp
Từ điểm A ở ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến (O) với B, C là các tiếp điểm. Kẻ một đường thẳng d nằm giữa hai tia AB, AO và đi qua A cắt đường tròn (O) tại E, F (E nằm giữa A, F).
1. Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.2. Gọi H là giao điểm của AD và BC. Chứng minh OH.OA = OE^2.3. Đường thẳng qua O vuông góc với EF cắt BC tại E. Chứng minh SF là tiếp tuyến của đường tròn (O).4. Đường thẳng SF cắt các đường thẳng AB và AC tương ứng tại P và Q. Đường thẳng OF cắt BC tại K. Chứng minh rằng AK đi qua trung điểm của PQ.cho đoạn thẳng OO 2cm a) vẽ đường tròn tâm O bán kính 1,5cm đường tròn này cắt đoạn thẳng OO tại C và cắt đường tròn OOở Db) Vẽ đường tròn tâm O bán kính 1cm , đường tròn này cắt đoạn OO tại E và cắt đg thẳng OO tại f Hai đường tròn trên đều cắt nhau tại a và b hãy kể tên dường kính của đường tròn (O,2cm) và đường kính đường tròn (O; 1,5 cm) và các dây cung của 2 dường tròn trên rồi tính các đường kính đó hãy chứng tỏ rằng e là trung điểm OO tính độ dài doạn thẳng DF6 tick nhoa mí bạn
Đọc tiếp
cho đoạn thẳng OO' =2cm
a) vẽ đường tròn tâm O bán kính 1,5cm đường tròn này cắt đoạn thẳng OO' tại C và cắt đường tròn OO'ở D
b) Vẽ đường tròn tâm O' bán kính =1cm , đường tròn này cắt đoạn OO' tại E và cắt đg thẳng OO' tại f
Hai đường tròn trên đều cắt nhau tại a và b
hãy kể tên dường kính của đường tròn (O,2cm) và đường kính đường tròn (O; 1,5 cm) và các dây cung của 2 dường tròn trên rồi tính các đường kính đó
hãy chứng tỏ rằng e là trung điểm OO'
tính độ dài doạn thẳng DF
6 tick nhoa mí bạn
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn. Qua A kẻ 2 đường thẳng cắt đường tròn (O) tại các điểm B,C và D,F tương ứng( B nằm giữa A và C, D nằm giữa A và E). Đường thẳng qua D và song song với BC cắt đường tròn (O) tại điểm thứ 2 F. Đường thẳng AF cắt đường tròn (O) tại điểm thứ 2 G. 2 đường thẳng EG và BC cắt nhau tại điểm M. CMR:a)AM2MG.MEb)ΔMGB∼ΔMCEc)frac{1}{AM}frac{1}{AB}+frac{1}{AC}
Đọc tiếp
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn. Qua A kẻ 2 đường thẳng cắt đường tròn (O) tại các điểm B,C và D,F tương ứng( B nằm giữa A và C, D nằm giữa A và E). Đường thẳng qua D và song song với BC cắt đường tròn (O) tại điểm thứ 2 F. Đường thẳng AF cắt đường tròn (O) tại điểm thứ 2 G. 2 đường thẳng EG và BC cắt nhau tại điểm M. CMR:
a)AM2=MG.ME
b)ΔMGB∼ΔMCE
c)\(\frac{1}{AM}=\frac{1}{AB}+\frac{1}{AC}\)
a) Do DF // AC nên \(\widehat{MAG}=\widehat{GFD}\) (Hai góc so le trong) .
Lại có \(\widehat{GFD}=\widehat{GED}\) (Hai góc nội tiếp cùng chắn cung GD)
Nên \(\widehat{MAG}=\widehat{GED}\)
Xét tam giác AMG và tam giác EMA có:
\(\widehat{MAG}=\widehat{MEA}\) (cmt)
Góc M chung
Vậy nên \(\Delta AMG\sim\Delta EMA\left(g-g\right)\Rightarrow\frac{MA}{ME}=\frac{MG}{MA}\Rightarrow MA^2=MG.ME\)
b) Do tứ giác ECBG nội tiếp nên \(\widehat{BCE}=\widehat{BGM}\) (Góc ngoài tại đỉnh đối của tứ giác nội tiếp)
Vậy xét tam giác MGB và MCE có:
\(\widehat{BGM}=\widehat{ECM}\left(cmt\right)\)
Góc M chung
Vậy nên \(\Delta MGB\sim\Delta MCE\left(g-g\right)\)
c) Theo câu a, ta có \(AM^2=MG.ME\)
Theo câu b, \(\Delta MGB\sim\Delta MCE\Rightarrow\frac{MG}{MC}=\frac{MB}{ME}\Rightarrow MG.ME=MB.MC\)
Vậy nên \(MA^2=MB.MC\)
Suy ra \(MA^2+MA.MC=MB.MC+MA.MC\)
\(\Leftrightarrow MA\left(MA+MC\right)=MC\left(MB+MA\right)\)
\(\Leftrightarrow MA.AC=MC.AB\)
\(\Leftrightarrow AB\left(AC-AM\right)=MA.AC\)
\(\Leftrightarrow AB.AC-AB.AM=AM.AC\)
\(\Leftrightarrow AB.AC=AM\left(AB+AC\right)\)
\(\Leftrightarrow\frac{1}{AM}=\frac{AB+AC}{AB.AC}\)
\(\Leftrightarrow\frac{1}{AM}=\frac{1}{AB}+\frac{1}{AC}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Từ điểm A nằm ngoài đường tròn (O), vẽ cát tuyến ABC với đường tròn. Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K. Qua K kẻ đường thẳng vuông góc với AO, cắt AO tại H và đường tròn (O) tại E và F (E nằm giữa K và F). Gọi M là giao điểm của OK và BC.gọi D là giao điểm của BC và EF chứng minh DB.AC =DC.AB
cho đường tròn tâm O và điểm A nằm ngoài đường tròn.một cát tuyến qua A cắt đường tròn (O) tại B và C( B nằm giữa A và C) các tiếp tuyến của (O) tại B và C cắt nhau tại D Đường thẳng D vuông góc với OA cắt (O) tại E và F( E nằm giưa D và F ) gọi M là giao điểm của DO và và BC


















