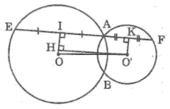
Kẻ OI ⊥ AE, O’K ⊥ AF
Trong đường tròn (O), ta có:
IA = IE = (1/2).AE (đường kính vuông góc với dây cung)
Trong đường tròn (O’), ta có:
KA = KF = (1/2).AF (đường kính vuông góc với dây cung)
Ta có: EF = AE = AF
Suy ra: EF = 2IA = 2AK = 2(IA + AK) = 2IK (1)
Kẻ O’H ⊥ OI
Khi đó tứ giác IHO’K là hình chữ nhật (có ba góc vuông)
Suy ra: O’H = IK
Trong tam giác OHO’ ta có: O’H ≤ OO’ = 3 (cm)
Suy ra: IK ≤ OO’ (2)
Từ (1) và (2) suy ra: EF ≤ 2OO’ = 6 (cm)
Ta có EF = 6cm khi H và O trùng nhau hay EF // OO’
Vậy EF có độ dài lớn nhất bằng 6cm khi và chỉ khi EF // OO’












