Cho tam giác ABC cân ở A có AB=8cm và nội tiếp trong đường tròn (O; 5cm).1) chứng minh .Tia đối của tia OA là tia phân giác của góc BOC.2) Gọi D là điểm đối xứng của A qua O. tính BD,BC.gửi hình vẽ vs lời giải giúp em nhá

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, đ tròn (O) ngoại tiếp tam giác ABC, đường tròn tâm (O') tiếp xúc trong với (O) và tiếp xúc với cạnh AB ở P, AC ở Q. Cm trung điểm I của PQ là tâm đ tròn nội tiếp tam giác ABC
1. Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R = 3cm. Tính diện tích hình quạt tạo bởi hai bán kính OB,OC và cung nhỏ BC khi \(\widehat{BAC}=60^o\)
2. Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm nội tiếp đường tròn (O). Tính diện tích hình tròn (O)
2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh AB = a, đường cao AH = h. Tính
bán kính đường tròn ngoại tiếp tam giác theo a và h.
Cho tam giác ABC cân tại A có AB = 8cm và nội tiếp đường tròn tâm O có bán kính bằng 5 cm. Vẽ đường kính AD cắt BC tại H. Tính BH và BC.
_Giúp mình với ,mình đang cần gấp <3
cho tam giác ABC vuông tạ A có AB = 6cm, ac = 8cm. Tính bán kính đường tròn ngoại tiếp R và bán kính đường tròn nội tiếp tam giác
trong tgiac vuông tâm đường tròn ngoại tiếp chính là trung điểm cạnh huyền
Áp dụng định lý pytago vào tgiac vuông ABC ta có :
\(BC^2\)=\(AC^2\)+\(AB^2\)
\(BC^2\)=\(8^2\)+\(6^2\)
\(BC^2\)=100
BC=10
Vậy bán kính đường tròn ngoại tiếp tgiac ABC là:
10:2=5cm
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tạ A có AB = 6cm, ac = 8cm. Tính bán kính đường tròn ngoại tiếp R và bán kính đường tròn nội tiếp tam giác
Gọi bk ngoại tiếp là R còn nôi tiếp là r ;p là 1/2 chu vi (= a+b+c/2)
ra có R=BC/2=5
mà S=pr=(6+8+10)/2r=6*8/2=>r=2
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC) nội tiếp trong đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng: Tam giác HAF cân
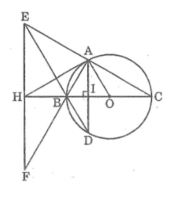
Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên: HA = HE = HF = (1/2).EF (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC) nội tiếp trong đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng: Tam giác EBF cân
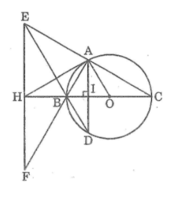
Gọi I là giao điểm của AD và BC
Vì BC là đường trung trực của AD nên theo tính chất đường trung trực ta có:
BA = BD
Tam giác BAD cân tại B có BI ⊥ AD nên BI là tia phân giác của góc ABD
Tam giác EBF có BH là tia phân giác của góc EBF và BH ⊥ EF nên tam giác EBF cân tại B.
Đúng 0
Bình luận (0)
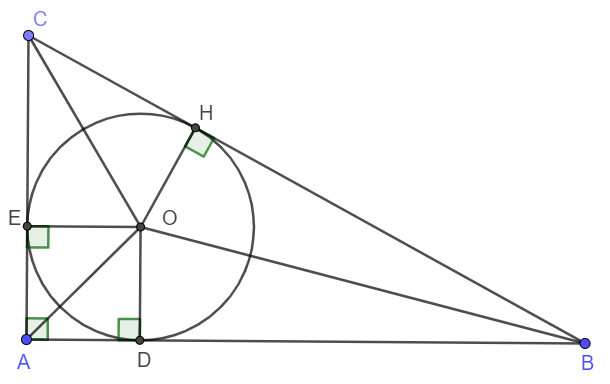
Cho tam giác $ABC$ vuông tại $A$. Đường tròn $(O)$ nội tiếp tam giác $ABC$ tiếp xúc với $AB$, $AC$ lần lượt tại $D$ và $E$.
a) Tứ giác $ADOE$ là hình gì?
b) Chứng minh \(S=p.r\) ($p$ là nửa chu vi tam giác $ABC$, $r$ là bán kính đường tròn nội tiếp).
b) Tính bán kính của đường tròn $(O)$ biết $AB = 6cm$, $AC = 8cm$.
BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr ( là chu vi của tam giác , là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).
giải:
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có
( là chu vi của tam giác , là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: .
Diện tích tam giác ABC là: .
Chu vi tam giác ABC là: .
Suy ra: .
Xem thêm câu trả lời



















