Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên: HA = HE = HF = (1/2).EF (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.
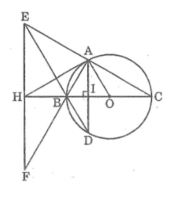
Cho tam giác ABC vuông tại A (AB < AC) nội tiếp trong đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng: Tam giác EBF cân
Cho tam giác ABC vuông tại A (AB < AC) nội tiếp trong đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng: HA là tiếp tuyến của đường tròn (O)
cho tam giác abc vuông tại a(ab<ac) nội tiếp (o;r) đường kính bc. Kẻ dây ad vuông góc với bc. gọi e là giao điểm của db và ca. qua e kẻ đường thẳng vuống góc với bc cắt bc tại h, cắt ab tại f. chứng minh rằng:
a) tam giác ebf cân
b) tam giác haf cân
c) ha là tiếp tuyến của (o)
Cho tam giác ABC nội tiếp trong đường tròn (O). Biết AB=4cm, BC=8,5cm và CA=7,5cm. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F.
a) Chứng minh tam giác ABC vuông và tính độ dài đường cao vẽ từ đỉnh góc vuông của tam giác ABC.
b) Chứng minh rằng EF=2AH.
c) Chứng minh rằng HA là tiếp tuyến của đường tròn (O).
Cho tam giác abc vuông tại a (AB<AC). Nội tiếp đường tròn tâm O đường kính BC. Kẻ dây AD vuông góc với BC. Gọi CA giao BD tại E. Qua E kẻ đường thẳng vuông góc với CB ở H., AB ở F. Chứng minh:
a, tam giác EBF cân.
b, Tam giác HAE cân.
c, HA là tiếp tuyến Của tâm O
Cho Tam giác ABC vuông tại A (AB <AC) nội tiếp đường tròn tâm O đường kính BC . Kẻ dây AD vuông góc với BC . Gọi E là giao điểm của DB và CA . Qua E kẻ đường thẳng vuông góc với BC , cắt BC tại H , cắt AB tại F
a,Cm : ∆HAF cân
b,CM : AB là tia phângiác góc HAD
c, CM : AC.CE=CB.CH
d,CM : C,D,F thẳng hàng
e, CM : AH là tiếp tuyến của (O)
g, gọi I là trung điểm AB . CM OI vuông góc với AB
Cho tam giác ABC có(AB<AC) nội tiếp (O) có BC là đường kính, kẻ dây AD vuông góc BC tại I,tia DB cắt tia CA tại E qua E kẻ đường thẳng vuông góc BC tại H, cắt tia AB tại F. chứng minh
a) tam giác abd cân
b)H,E,A,B cùng thuộc một đường tròn
c)tam giác HAF cân
d) B cách đều 3 cạnh tam giác HAD
HELPPPPPPPPPPPP
Cho tam giác ABC nội tiếp đường tròn tâm o (AB<AC) diemrd M l;à trung điểm của cạnh BC . đường phân giác trong góc BAC cắt BC ở D vá cắt đường tròn O ở P ( P khác A ) GỌI E đối xững với D qua M .qua D kẻ đường thẳng vuông góc với BC cắt AO ở H qua E kẻ đường vuông góc với BC cắt AD ở F .gọi K là giao cảu PE và DH
1)CHỨNG MINH TỨ GIÁC DEFK LÀ HÌNH CHỮ NHẬT
2)CHỨNG MINH DB.DC=DA.DP=DH.DK TỪ ĐÓ SUY RA BHCK NỘT TIẾP ĐƯỜNG TRÒN TAM I
3)GỌI T LÀ GIAO AD VÀ (I)9T KHÁC F) CHỨNG MINH HT VUÔNG GÓC VỚI AD
4)ĐƯỜNG TRÒN NGOẠI TIẾP TAM GIÁC MTP CẮT TH Ở Q ( KHÁC T) CHỮNG MINH QA TIẾP XÚC VỚI (O)
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O, R) có BC là đường kính và AC=R. Kẻ dây AD vuông góc với BC tại H.
1) Tính độ dài các cạnh AB, AH theo R;
2) Chứng minh rằng HA.HD=HB.HC;
3) Gọi M là giao điểm của AC và BD. Qua M kẻ đường thẳng vuông góc với BC cắt BC ở I, cắt AB ở N. Chứng minh ba điểm N, C, D thẳng hàng;
4) Chứng minh AI là tiếp tuyến của đường tròn (O, R).
