Cho số thực z 1 và số phức z 2 thoả mãn | z 2 -2i|=1 và z 2 - z 1 1 + i là số thực. Gọi a, b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của | z 1 - z 2 |. Tính T=a+b.
A. T = 4
B. T = 4 2
C. T = 3 2 + 1
D. T = 2 + 3
Cho số phức z thoả mãn (2+z)i=3-2i. Phần thực của z bằng
A. -2.
B. -3.
C. -4.
D. -5.
Cho số phức Z thoả mãn (1+2i)z-5= 3i tìm số phức liên hợp z 2/ cho số phức z=a+bi(a, b thuộc R) thoả mãn 3z-5z ngan -6+10i=0 .tính a-b
\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)
\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)
\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)
2.
Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?
Cho các số phức z thoả mãn z = 2 . Đặt w = ( 1 + 2 i ) z - 1 + 2 i . Tìm giá trị nhỏ nhất của w
A. 2
B. 3 5
C. 2 5
D. 5
Cho số phức z thoả mãn z + z ¯ ≤ 2 và z − z ¯ ≤ 2 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của T = z − 2 i . Tổng M + m bằng
A. 1 + 10 .
B. 2 + 10 .
C. 4 .
D. 1 .
Cho số phức z=a+bi a , b ∈ R thỏa mãn z = 5 và z ( 2 + i ) ( 1 - 2 i ) là một số thực. Tính P = a + b .
A. P=5
B. P=7
C. P=8
D. P=4
Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)2(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?
A. -3; -2
B. 2; 3
C. 2; -3
D. Đáp án khác.
Chọn C.
Ta có: ( 1 + i)2(2 - i) z = 8 + i + (1 + 2i)z
Nên z[( 1 + i)2(2 -i) – (1 + 2i) ] = 8 + i
Suy ra: z[2i(2 - i) – 1 - 2i] = 8 + i
![]()
Vậy số phức z đã cho có phần thực là 2, phần ảo là -3.
Cho số phức z thoả mãn |z – 1 + 3i| + |z + 2 – i| = 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = |2z + 1 = 2i|.
A. 8 và 4
![]()
![]()
![]()
Chọn D.
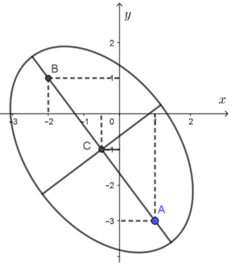
Ta có P = |2z + 1 = 2i| nên 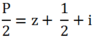
Ta cần tìm giá trị lớn nhất, giá trị nhỏ nhất của: 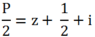
Ta có z1 = 1 - 3i; z2 = -2 + i và z0 = -1/2 - i
Ta thấy: ![]()
Tính 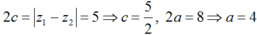
Suy ra 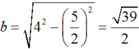
Vậy Max P = 2.4 = 8 và 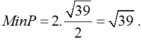
Gọi S là tập hợp tất cả các số phức z thoả mãn z - 1 = 34 và z + 1 + m i = z + m + 2 i . Gọi z1, z2 là hai số phức thuộc (S) sao cho z 1 - z 2 nhỏ nhất, giá trị của z 1 + z 2 bằng
A.2
B. 2 3
C. 2
D. 3 2
Cho số phức z = a+bi(a,b ϵ ℝ) thỏa mãn |z|=5z và z(2+i)(1-2i) là một số thực. Tính giá trị P=|a|+|b|
A.P=8
B.P=4
C.P=5
D. P=7
Tìm tổng phần thực và phần ảo của số phức z thỏa mãn: (1 - i) ( z - 2i) = 2 + i.
A. 4.
B. 3.
C. 5.
D. 7.