Trong không gian cho ba điểm A, B, C.
Xác định điểm G sao cho: G A → + 2 G B → - 2 G C → = 0 →
Những câu hỏi liên quan
Trong không gian cho đường thẳng a và A, B, C, E, F, G là các điểm phân biệt và không có ba điểm nào trong đó thẳng hàng. Khẳng định nào sau đây đúng A.
a
//
B
C
B
C
⊂
E
F
G...
Đọc tiếp
Trong không gian cho đường thẳng a và A, B, C, E, F, G là các điểm phân biệt và không có ba điểm nào trong đó thẳng hàng. Khẳng định nào sau đây đúng
A. a // B C B C ⊂ E F G ⇒ a // E F G
B. a ⊥ B C a ⊥ A C ⇒ a ⊥ m p A B C
C. A B // E F B C // F G ⇒ A B C // E F G
D. a ⊥ A B C a ⊥ E F G ⇒ A B C // E F G
Chọn B
Đáp án A sai do đường thẳng a có thể nằm trong mặt phẳng (EFG).
Đáp án C sai do mặt phẳng (ABC) có thể trùng với mặt phẳng (EFG).
Đáp án D sai do mặt phẳng (ABC) có thể trùng với mặt phẳng (EFG).
Đúng 0
Bình luận (0)
Cho ba điểm A(-1; 1), B(1;5), G(1 ; 2).
a) Chứng minh ba điểm A, B, G không thẳng hàng.
b) Tìm toạ độ điểm C sao cho G là trọng tâm của tam giác ABC.
a) Ta có: \(\overrightarrow {AB} = \left( {2;4} \right),\overrightarrow {AG} = \left( {2;1} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AG} \) nên A, B, G không thẳng hàng
b) Giả sử C có tọa độ là: \(C\left( {{x_C};{y_C}} \right)\)
Để G là trọng tâm tam giác ABC thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B}\\{y_C} = 3{y_G} - {y_A} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3.1 - \left( { - 1} \right) - 1 = 3\\{y_C} = 3.2 - 1 - 5 = 0\end{array} \right.\)
Vậy tọa độ điểm C là: \(C\left( {3;0} \right)\)
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;-3;2), B(0;1;-2) và G(2;-1;1). Tọa độ điểm C sao cho tam giác ABC nhận G là trọng tâm là A.
C
1
;
-
1
;
2
3
B. C(3;-3;2) C. C(5;-1;2) D. C(1;1;0)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;-3;2), B(0;1;-2) và G(2;-1;1). Tọa độ điểm C sao cho tam giác ABC nhận G là trọng tâm là
A. C 1 ; - 1 ; 2 3
B. C(3;-3;2)
C. C(5;-1;2)
D. C(1;1;0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;-3;2), B(0;1;-1) và G(2;-1;1). Tọa độ điểm C sao cho tam giác ABC nhận G là trọng tâm là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;-3;2), B(0;1;-1) và G(2;-1;1). Tọa độ điểm C sao cho tam giác ABC nhận G là trọng tâm là:
Trong không gian Oxyz , cho điểm
G
-
1
;
2
;
-
1
.
Mặt phẳng (a) đi qua G và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho G là trọng tâm của DABC . Điểm nào sau đây thuộc mặt phẳng (a) ? A.
N
-
3
;
4...
Đọc tiếp
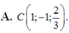
Trong không gian Oxyz , cho điểm G - 1 ; 2 ; - 1 . Mặt phẳng (a) đi qua G và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho G là trọng tâm của DABC . Điểm nào sau đây thuộc mặt phẳng (a) ?
A. N - 3 ; 4 ; 2
B. P - 3 ; - 4 ; 2
C. Q 3 ; 4 ; 2
D. M 3 ; 4 ; - 2
Cho đa thức G(x)=ax2 + bx + c.Xác định các hệ số a, b, c biết G(2)=6; G(-2)=18 và a - c = -2.
Trong không gian Oxyz, cho ba điểm
A
(
3
;
3
;
7
)
,
B
(
2
;
3
;
2
)
và
C
(
-
2
;
-
3
;
3
)
. Toạ độ trọng tâm G của tam giác ABC là
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A ( 3 ; 3 ; 7 ) , B ( 2 ; 3 ; 2 ) và C ( - 2 ; - 3 ; 3 ) . Toạ độ trọng tâm G của tam giác ABC là
Trong không gian Oxyz, cho ba điểm
A
(
1
;
0
;
-
2
)
,
B
(
2
;
1
;
-
1
)
,
C
(
1
;
-
2
;
2
)
. Tìm tọa độ trọng tâm G của tam giác ABC
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A ( 1 ; 0 ; - 2 ) , B ( 2 ; 1 ; - 1 ) , C ( 1 ; - 2 ; 2 ) . Tìm tọa độ trọng tâm G của tam giác ABC
Trong không gian Oxyz , cho điểm G(-1;2;-1). Mặt phẳng
α
đi qua G và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho G là trọng tâm của DABC . Điểm nào sau đây thuộc mặt phẳng
α
?
Đọc tiếp
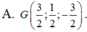
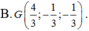
Trong không gian Oxyz , cho điểm G(-1;2;-1). Mặt phẳng α đi qua G và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho G là trọng tâm của DABC . Điểm nào sau đây thuộc mặt phẳng α ?
