Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng:
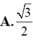
![]()
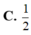
![]()
Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng
A. 3 2
B. 3
C. 1 2
D. 1
Chọn C.
Phương pháp:
Công thức tính diện tích mặt cầu bán kính R là: S = 4 π R 2 .
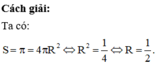
Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là
A. 2 3
B. 3
C. 1
D. 1 2
Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là
![]()
![]()
![]()
![]()
Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là
A. 2/3
B. 3
C. 1
D. 1/2
Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán kính a. Khi đó thể tích của hình trụ bằng
A. S a
B. 1 2 S a
C. 1 3 S a
D. 1 4 S a
Một hình trụ có diện tích xung quanh bằng S, diện tích đáy bằng diện tích một mặt cầu bán kính a. Khi đó thể tích của hình trụ bằng:
A. Sa
B. 1 2 Sa
C. 1 3 Sa
D. 1 4 Sa
Chọn A.
Gọi r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.
Theo bài ra ta có:
S = 2 π r h π r 2 = 4 π a 2 ⇔ r = 2 a h = S 4 π a
Thể tích khối trụ là:
V = π r 2 h = π 4 a 2 · S 4 π a = S a
Một khối trụ có thể tích bằng 25 π . Nếu chiều cao khối trụ tăng lên năm lần và giữ nguyên bán kính đáy thì khối trụ mới có diện tích xung quanh bằng 25. Bán kính đáy của khối trụ ban đầu là:
A. r = 10
B. r = 5
C. r = 2
D. r = 15
Một hình trụ có bán kính đáy là 5cm, diện tích xung quanh bằng 300 π ( c m 2 ). Chiều cao của hình trụ là?
A. 6cm
B. 12cm
C. 30cm
D. 10cm
Đáp án A
Gọi chiều cao của hình trụ là h
Ta có:
S x q = 2 π R 2 h ⇔ 2 π . 5 2 . h = 300 π ⇒ h = 6 ( c m )
Câu 1: Thể tích hình trụ là 375 π , chiều cao 15. Tính diện tích xung quanh hình trụ.
Câu 2: Một hình trụ có diện tích toàn phần bằng diện tích hình tròn có bán kính 12cm, chiều cao hình trụ bằng 2 lần bán kính đáy. Tính bán kính đáy hình trụ đó.
1:
V=pi*r^2*h
=>r^2*15*pi=375pi
=>r^2=25
=>r=5
Sxq=2*pi*r*h=2*5*15*pi=150pi