Tính khoảng cách h từ A 1 ; - 2 ; 4 tới mặt phẳng P : - 3 x + 4 z + 1 = 0
![]()
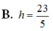
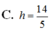
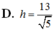
Khoảng cách d (tính bằng km) từ một người ở vị trí có chiều cao h ( tính bằng m) là khoảng cách từ mực nước biển đến mắt người quan sát nhìn thấy được đường chân trời được tính theo công thức d h = 3,57 , a) Hãy tính khoảng cách d từ người đó đến đường chân trời, biết người đó đang đứng trên ngọn hải đăng Kê gà có chiều cao của tầm mắt là 65 m so với mực nước biển (kết quả làm tròn đến chữ số thập phân thứ hai ) b) Muốn nhìn được đường chân trời từ khoảng cách 25 km thì vị trí quan sát của ngọn hải đăng phải xây cao bao nhiêu so với mực nước biển ? ( kết quả làm tròn đến chữ số thập phân thứ hai).
1)xác định đường vuông góc,đường xiên kẻ từ điểm h đến điểm DC
2)so sánh AD và AE
3)tính khoảng cách từ điểm a đến đường thẳng DC
4)so sánh AD và AE
6)tính khoảng cách từ điểm C đến đường thẳng AD
7)so sánh AE và AF
biết ABCD là hình chữ nhật
2: ΔADE vuông tại D
nên AD<AE
3: h(A;DC)=AD
6: h(C;AD)=CD
7: góc AED<90 độ
=>góc AEF>90 độ
=>AE<AF
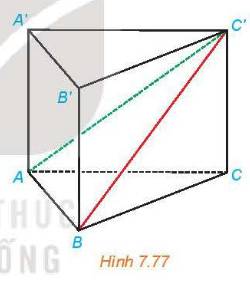
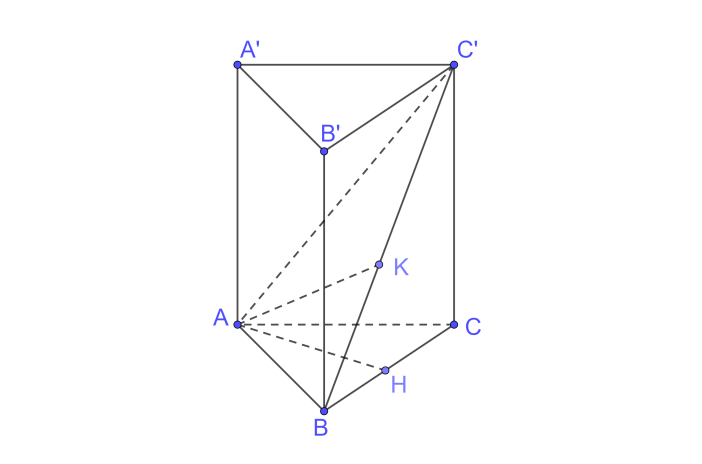
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77).
a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').
b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.
a) Ta có \(BB' \bot \left( {ABC} \right);BB' \subset \left( {BCC'B'} \right) \Rightarrow \left( {ABC} \right) \bot \left( {BCC'B'} \right)\)
\(\left( {ABC} \right) \cap \left( {BCC'B'} \right) = BC\)
(ABC): Kẻ \(AH \bot BC\)
\( \Rightarrow AH \bot \left( {BCC'B'} \right) \Rightarrow d\left( {A,\left( {BCC'B'} \right)} \right) = AH\)
Xét tam giác ABC vuông cân tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{2}{{{a^2}}}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow AH = \frac{{a\sqrt 2 }}{2}\)
b) +) Ta có \(AB \bot AC,AB \bot AA'\left( {AA' \bot \left( {ABC} \right)} \right) \Rightarrow AB \bot \left( {ACC'A'} \right);AC' \subset \left( {ACC'A'} \right) \Rightarrow AC' \bot AB\)
Do đó tam giác ABC' là tam giác vuông.
+) Trên (ABC’) kẻ \(AK \bot BC' \Rightarrow d\left( {A,BC'} \right) = AK\)
Xét tam giác ACC’ vuông tại C có
\(A{C'^2} = A{C^2} + C{C'^2} = {a^2} + {h^2}\) (Định lí Pytago)
Xét tam giác ABC’ vuông tại A có
\(\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{{C'}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2} + {h^2}}} = \frac{{2{a^2} + {h^2}}}{{{a^2}\left( {{a^2} + {h^2}} \right)}} \Rightarrow A{K^2} = \frac{{{a^2}\left( {{a^2} + {h^2}} \right)}}{{2{a^2} + {h^2}}}\\ \Rightarrow AK = a.\sqrt {\frac{{{a^2} + {h^2}}}{{2{a^2} + {h^2}}}} \end{array}\)
Tính khoảng cách h từ A - 4 ; 1 ; 2 tới mp(Ozx).
![]()
![]()
![]()
![]()
Cùng 1 lúc có 2 xe từ 2 địa điểm A và B cách nhau 20km chuyển động cùng chiều theo hướng từ A về B xe thứ nhất khởi hành từ A với vận tốc 30km/h ,xe thứ 2 khởi hành từ B với vận tốc là 40km/h a) tính khoảng cách giữa 2 xe sao 1 h kể từ lúc xúc phát b) sau khi xúc phát được 1giờ 30 phút ,xe thứ nhất đột ngột tăng tốc lên đến 50km/h ,xác định thời gian và vị trí 2 xe gặp nhau
a)sau 1h xe đi từ A đi được số km là
sA=vA.t=30.1=30km
sau 1h xe thứ 2 đi được số km là
sB=vB.t=40.1=40km
khoảng cách giữa 2 xe là
Δs=sAB+(SB-SA)=30km
b)sA=vA.1,5=45km
sB=vB.1,5=60km
Δs=AB+(sB-sA)=35km
sA'=vA'.t=50t
sB'=vB.t=40t
sA'-sB'=Δs
50t-40t=35
10t=35
t=35:10=3,5h
1 ca nô xuôi dòng từ A đến B mất 2,5h và ngược dòng từ B về A mất 4h. Bt V dòng nước 3km/h. Tính khoảng cách AB.
Gọi x là vận tốc thực của ca nô (x>3)
-vận tốc xuôi dòng: x+3(km/h) \(\rightarrow\)S=(x+3).2,5 (km)
-vận tốc ngược dòng: x-3(km/h)\(\rightarrow\)S=(x-3).4(km)
ta có phương trình: (x-3).4=(x+3).2,5
\(\Leftrightarrow\)4x-12=2,5x+7,5
\(\Leftrightarrow\)x=13 (thỏa mãn x>3)
S=(x-3).4=(13-3).4=40(km)
Một vật AB có độ cao h = 2cm đặt vuông góc với trục chính của một TKHT tiêu cự f = 15cm và cách TK một khoảng OA Trường hợp 1: OA= 10cm < f ; a. Dựng ảnh A’B’ của AB tạo bởi TKHT đã cho? b. Tính khoảng cách từ ảnh đến TKHT ? c. Tính chiều cao h’ của ảnh ? d. Nếu ảnh cao gấp 3 lần vật thì khoảng cách từ ảnh đến TK là bao nhiêu? e. Tính khoảng cách vật đến ảnh ? f.Nếu di chuyển vật AB đến vị trí mới cách vị trí cũ một đoạn 5cm (A vẫn nằm trên trục chính) thì ảnh A’B’ sẽ di chuyển một đoạn bằng bao nhiêu cm so với vị trí ban đầu của nó ?(chia ra 2 trường hợp: lại gần và ra xa TK)
một ô tô chạy từ địa điểm a đến địa điểm b với tốc độ 65km/h, cùng lúc dó 1 xe máy đi từ b về a với lận tốc 40km/h. Biết khoảng cách ab là 540 km và M là trung điểm của ab. Hỏi sau bao lâu thì ô tô cách M 1 khoảng bằng 1/2 khoảng cách từ xe máy đến M
Theo bài ra ta có: quãng đường AB dài 540km => Nửa quãng đường AB dài 270km.
Gọi quãng đường ô tô và xe máy đã đi là S1 và S2.
Trong cùng một thời gian thì quãng đường tỉ lệ thuận với vận tốc.
\(\dfrac{S_1}{V_1}=\dfrac{S_2}{V_2}=t\)
Ta có phương trinh:
\(\dfrac{270-a}{65}=\dfrac{270-a}{40}\Rightarrow t=\dfrac{270}{90}=3h\)
Vậy sau 3 giờ thì ô tô cách M 1 khoảng bằng 1/2 khoảng cách xe máy đến M
Hai xe ô tô khởi hành cũng 1 lúc , 1 tại A và 1 tại B để đi đến C . A cách B 60km và B nằm giữa A và C đi từ A là 80km/h còn xe đi từ B có vận tốc 65km/h . Hai xe đến C cùg 1 lúc . Tính khoảng cách BC
Hai xe khởi hành cùng 1 lúc 1- A; 1- B để về C. A cách B 60km. B nằm giữa A và C. Vận tốc xe đi từ A là 80 km/h. Vận tốc xe đi từ B là 65km/h. Hai xe đến C cùng 1 lúc. Tính khoảng cách BC.