Tìm một vectơ pháp tuyến của mặt phẳng (P) chứa A 0 ; - 1 ; 1 và B 1 ; 2 ; 0 sao cho 2 điểm E - 1 ; 2 ; 4 và F 3 ; 0 ; - 2 thuộc về hai phía của (P) và khoảng cách từ E tới mặt phẳng (P) bằng khoảng cách từ F tới mặt phẳng (P).
Những câu hỏi liên quan
Cho
P
:
x
+
y
-
2
z
-
4
0
;
A
-
1
;
0
;
1
. Biết mặt phẳng (Q) chứa O và A, đồng thời
Q
⊥
P
. Tìm một vectơ pháp tuyến
n
→
của (Q).
Đọc tiếp
Cho P : x + y - 2 z - 4 = 0 ; A - 1 ; 0 ; 1 . Biết mặt phẳng (Q) chứa O và A, đồng thời Q ⊥ P . Tìm một vectơ pháp tuyến n → của (Q).
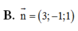
Tìm một vectơ pháp tuyến của mặt phẳng (P): 2x-3y+z=0
A. (-2;-3;1)
B. (2;-3;1)
C. (2;-3;0)
D. (2;-3;-1)
Trong không gian Oxyz, cho mặt phẳng (P): x - 2y + 2z - 7 = 0. Tìm một vectơ pháp tuyến n → của mặt phẳng (P).
A. (-1;2;-2)
B. (1;2;2)
C. (-2;-4;4)
D. (2;-4;-4)
Trong không gian Oxyz, mặt phẳng (P): x-2z+3=0. Tìm một vectơ pháp tuyến của (P)
A. n → =(1;-2;3)
B. n → =(1;0;-2)
C. n → =(1;-1;0)
D. n → =(0;1;0)
Trong không gian Oxyz, mặt phẳng (P): 2x+y-z+1=0. Tìm một vectơ pháp tuyến của (P)
A. (-4;2;6)
B. (2;1;3)
C. (-6;-9;9)
D. (6;-3;-9)
Trong không gian Oxyz, mặt phẳng (P): 3x+2y-z+1=0. Tìm một vectơ pháp tuyến của (P)
A. (-1;3;2)
B. (3;-1;2)
C. (2;3;-1)
D. (3;2;-1)
Trong không gian Oxyz, mặt phẳng (P): 2x+3y-4z+5=0. Vectơ nào sau đây là một vectơ pháp tuyến của mặt phẳng (P)
A. (-4;3;2)
B. (2;3;4)
C. (2;3;5)
D. (2;3;-4)
Cho mặt phẳng (P): x - 2y + 3z - 1 = 0. Một vectơ pháp tuyến của mặt phẳng (P) là
A. (1;2;3)
B. (1;-2;3)
C. (1;3;-2)
D. (1;-2;-3)
Cho mặt phẳng
P
:
2
x
-
y
-
z
+
1
0
. Gọi (Q) là mặt phẳng vuông góc với (P), (Q) đi qua
O
0
;
0
;
0
và
A
2
;
3
;
2
. Tìm một v...
Đọc tiếp
Cho mặt phẳng P : 2 x - y - z + 1 = 0 . Gọi (Q) là mặt phẳng vuông góc với (P), (Q) đi qua O 0 ; 0 ; 0 và A 2 ; 3 ; 2 . Tìm một vectơ pháp tuyến của (Q).
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình là x - 2y + 2 0. Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P): A.
n
1
→
1
;
-
2
;
2
B.
n
2
→...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình là x - 2y + 2 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P):
A. n 1 → = 1 ; - 2 ; 2
B. n 2 → = 1 ; - 2 ; 1
C. n 3 → = 1 ; - 2 ; 0
D. n 4 → = 1 ; 0 ; - 2
Đáp án C
Mặt phẳng (P) có phương trình là x - 2y + 2 = 0. Một vectơ pháp tuyến của mặt phẳng (P): n 3 → = (1; -2; 0)
Đúng 0
Bình luận (0)