Tính khoảng cách h từ A - 4 ; 1 ; 2 tới mp(Ozx).
![]()
![]()
![]()
![]()
Khoảng cách d (tính bằng km) từ một người ở vị trí có chiều cao h ( tính bằng m) là khoảng cách từ mực nước biển đến mắt người quan sát nhìn thấy được đường chân trời được tính theo công thức d h = 3,57 , a) Hãy tính khoảng cách d từ người đó đến đường chân trời, biết người đó đang đứng trên ngọn hải đăng Kê gà có chiều cao của tầm mắt là 65 m so với mực nước biển (kết quả làm tròn đến chữ số thập phân thứ hai ) b) Muốn nhìn được đường chân trời từ khoảng cách 25 km thì vị trí quan sát của ngọn hải đăng phải xây cao bao nhiêu so với mực nước biển ? ( kết quả làm tròn đến chữ số thập phân thứ hai).
Cho tứ diện ABCD có AC=AD=BC=BD, AB=a, CD= a 3 Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Cho tứ diện ABCD có A B = A D = B C = B D , A B = a , C D = a 30 . Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó.
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Chọn B
Gọi I là trung điểm AB, J là trung điểm CD
Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD
=> IJ = a
Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD
=> O nằm trên IJ => Ta cần tính OA
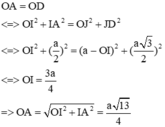
Ta có:
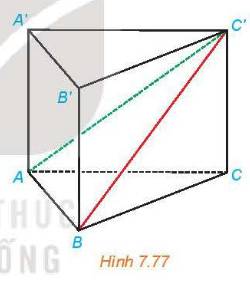
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77).
a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').
b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.
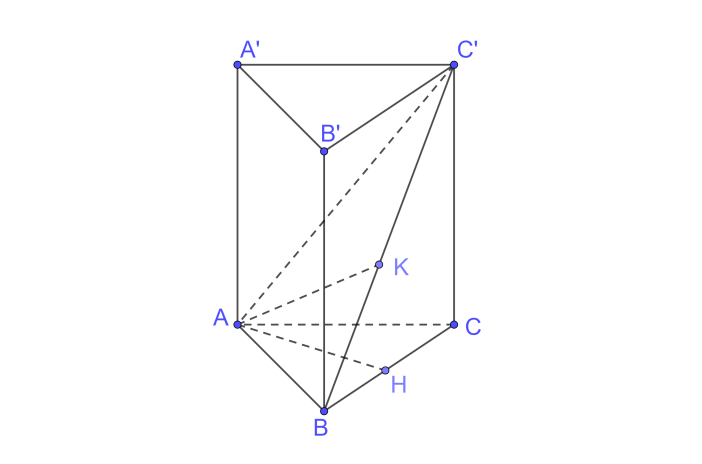
a) Ta có \(BB' \bot \left( {ABC} \right);BB' \subset \left( {BCC'B'} \right) \Rightarrow \left( {ABC} \right) \bot \left( {BCC'B'} \right)\)
\(\left( {ABC} \right) \cap \left( {BCC'B'} \right) = BC\)
(ABC): Kẻ \(AH \bot BC\)
\( \Rightarrow AH \bot \left( {BCC'B'} \right) \Rightarrow d\left( {A,\left( {BCC'B'} \right)} \right) = AH\)
Xét tam giác ABC vuông cân tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{2}{{{a^2}}}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow AH = \frac{{a\sqrt 2 }}{2}\)
b) +) Ta có \(AB \bot AC,AB \bot AA'\left( {AA' \bot \left( {ABC} \right)} \right) \Rightarrow AB \bot \left( {ACC'A'} \right);AC' \subset \left( {ACC'A'} \right) \Rightarrow AC' \bot AB\)
Do đó tam giác ABC' là tam giác vuông.
+) Trên (ABC’) kẻ \(AK \bot BC' \Rightarrow d\left( {A,BC'} \right) = AK\)
Xét tam giác ACC’ vuông tại C có
\(A{C'^2} = A{C^2} + C{C'^2} = {a^2} + {h^2}\) (Định lí Pytago)
Xét tam giác ABC’ vuông tại A có
\(\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{{C'}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2} + {h^2}}} = \frac{{2{a^2} + {h^2}}}{{{a^2}\left( {{a^2} + {h^2}} \right)}} \Rightarrow A{K^2} = \frac{{{a^2}\left( {{a^2} + {h^2}} \right)}}{{2{a^2} + {h^2}}}\\ \Rightarrow AK = a.\sqrt {\frac{{{a^2} + {h^2}}}{{2{a^2} + {h^2}}}} \end{array}\)
Một ca nô xuôi dòng từ A đến B mất 4 giờ và từ B về A mất 5 giờ . Tính khoảng cách AB , biết vận tốc dòng nước 2km/h.
Câu 16: Khoảng cách từ ảnh của vật đến gương phẳng có tính chất nào sau đây?
A. Bằng khoảng cách từ vật đến gương
B. Nhỏ hơn khoảng cách vật đến gương
C. Lớn gấp 2 lần khoảng cách từ vật đến gương
D. Lớn gấp 4 lần khoảng cách từ vật đến gương
Câu 17: Ảnh của vật tạo bởi gương cầu lồi có tính chất nào sau đây?
A. Ngược chiều so với vật B. Cùng chiều so với vật
C. Gương to thì ảnh cùng chiều với vật D. Gương nhỏ thì ảnh ngược chiều với vật
Câu 18: Ảnh của vật tạo bởi gương cầu lõm có tính chất nào sau đây?
A. Ngược chiều so với vật B. Cùng chiều so với vật
C. Gương to thì ảnh cùng chiều với vật D. Gương nhỏ thì ảnh ngược chiều với vật
Câu 19: Ảnh ảo của vật tạo bởi gương cầu lõm luôn?
A. Lớn bằng vật B. Nhỏ hơn vật C. Lớn hơn vật
Câu 20: Âm thanh được tạo ra nhờ:
A. Nhiệt B. Điện C. Ánh sáng D. Dao động
Câu 21: Số dao động trong một giây gọi là?
A. Độ dài B. Tần số C. Khối lượng D. Trọng lượng
Câu 16: Khoảng cách từ ảnh của vật đến gương phẳng có tính chất nào sau đây?
A. Bằng khoảng cách từ vật đến gương
B. Nhỏ hơn khoảng cách vật đến gương
C. Lớn gấp 2 lần khoảng cách từ vật đến gương
D. Lớn gấp 4 lần khoảng cách từ vật đến gương
Câu 17: Ảnh của vật tạo bởi gương cầu lồi có tính chất nào sau đây?
A. Ngược chiều so với vật B. Cùng chiều so với vật
C. Gương to thì ảnh cùng chiều với vật D. Gương nhỏ thì ảnh ngược chiều với vật
Câu 18: Ảnh của vật tạo bởi gương cầu lõm có tính chất nào sau đây?
A. Ngược chiều so với vật B. Cùng chiều so với vật
C. Gương to thì ảnh cùng chiều với vật D. Gương nhỏ thì ảnh ngược chiều với vật
Câu 19: Ảnh ảo của vật tạo bởi gương cầu lõm luôn?
A. Lớn bằng vật B. Nhỏ hơn vật C. Lớn hơn vật
Câu 20: Âm thanh được tạo ra nhờ:
A. Nhiệt B. Điện C. Ánh sáng D. Dao động
Câu 21: Số dao động trong một giây gọi là?
A. Độ dài B. Tần số C. Khối lượng D. Trọng lượng
một chiếc thuyền xuôi từ a đến b rồi ngược từ b về a hết 45 phút tính khoảng cách ab biết rằng vận tốc của thuyền khi xuôi dòng là 8km/h và khi ngược dòng là 4 km/h
theo đề ta có : vận tốc khi đi từ a đến b gấp 2 lần vận tốc đi về nên thời gian đi và về cũng vậy
ta có sơ đồ : bn tự vẽ
tổng số phần bằng nhau là :
2 + 1 = 3 ( phần )
thời gian khi đi là :
45 : 3 x 1 = 15 ( phút )
khoảng cách AB là :
15 x 8 = 120 ( km )
Đáp số : 120 km
Tỉ số giữa vận tốc xuối dòng và ngược dòng là \(\frac{8}{4}=\frac{1}{2}\)
=> Ta có thời gian đi xuôi dòng là:
45 : ( 1 + 2 ) . 1 = 15 ( phút ) = 0,25 giờ.
=> Quãng đường ab là:
8 . 0,25 = 2 ( km )
Đ/s: 2 km.
P/s: Bạn kia làm sai rồi. Mk nghĩ thế thôi, sai thì xin lỗi nha.
~ Hok tốt ~
Gọi quãng đường AB là S
Ta có công thức : S = V \(\times\)t
=> t = \(\frac{S}{V}\) => t(ngược dòng) = \(\frac{S}{V\left(ngược\right)}\)= \(\frac{S}{4}=S\times\frac{1}{4}\left(1\right)\)
=> t(xuôi dòng) = \(\frac{S}{V\left(xuoi\right)}\)= \(\frac{S}{8}=S\times\frac{1}{8}\left(2\right)\)
mà t(xuôi dòng) + t(ngược dòng) = 45 phút = 3/4 giờ (3)
Thay (1) và (2) vào (3) ta có :
\(S\times\frac{1}{8}+S\times\frac{1}{4}=\frac{3}{4}\)
\(\Rightarrow S\times\left(\frac{1}{8}+\frac{1}{4}\right)=\frac{3}{4}\)
\(\Rightarrow S\times\frac{3}{8}=\frac{3}{4}\)
\(\Rightarrow S=\frac{3}{4}:\frac{3}{8}\)
\(\Rightarrow S=2\left(km\right)\)
Vậy đoạn AB dài 2 km
Một sà lan xuôi dòng từ A đến B mất 2,5 giờ và ngược dòng từ B về A mất 4 giờ. Biết vận tốc dòng nước là 3km/h. Tính khoảng cách AB
gọi khoảng cách AB là x [ km ] [ x lớn hơn 0 ]
vận tốc đi xuôi dòng từ A đến B là \(\frac{x}{2,5}\)[ km/h ]
vận tốc đi ngược dòng từ B về A là \(\frac{x}{4}\)[ km/h ]
vận tốc thực đi xuôi dòng từ A đến B là \(\frac{x}{2,5}\)- 3 [ km/h ]
vận tốc thực đi ngược dòng từ B về A là \(\frac{x}{4}\)+ 3 [ km/h ]
theo bài toán , ta có phương trình
\(\frac{x}{2,5}\)- 3 = \(\frac{x}{4}\)+ 3
\(\frac{x-7,5}{2,5}\)=\(\frac{x+12}{4}\)
4[ x - 7,5 ] = 2,5[ x + 12 ]
4x - 30 = 2,5x + 30
4x - 2,5x = 30 + 30
[ 4 - 2,5 ]x = 60
1,5x = 60
x = 60 ; 1,5 ; là dấu chia nhé
x = 40 [ km ]
vậy khoảng cách AB là 40km
CHÚC BẠN HỌC TỐT
Nhớ kết bạn với mình đó
Một ca nô xuôi dòng từ A đến B mất 4 giờ và ngược dòng từ B về A mất 5 giờ. Tính khoảng cách AB, biết rằng vận tốc dòng nước là 2km/h
Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.
Vì vận tốc xuôi dòng lớn hơn vận tốc ngược dòng chính bằng 2 lần vận tốc dòng nước nên ta có phương trình:
x = 80 (thỏa mãn điều kiện).
Vậy khoảng cách giữa hai bến A và B là 80km.
(Giải thích tại sao hiệu vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước:
Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có:
Khi xuôi dòng: vận tốc canô = v + a
Khi ngược dòng: vận tốc canô = v - a
Hiệu vận tốc = v + a - (v - a) = 2a = 2 vận tốc dòng nước.)
Gọi vận tốc thực cano là x ( km/h, > 0 )
Vận tốc ngược dòng : x - 2 km/h
Vận tốc xuôi dòng : x + 2 km/h
Quãng đường từ AB khi đi ngược dòng : 5( x - 2 ) km
Quãng đường từ AB khi đi xuôi dòng : 4( x + 2 ) km
Vì quãng đường ko đổi nên ta có phương trình
\(5\left(x-2\right)=4\left(x+2\right)\Leftrightarrow5x-10=4x+8\Leftrightarrow x=18\)km/h
Quãng đường AB dài : \(4\left(18+2\right)=4.20=80\)km
Gọi x (km/h) là vận tốc của cano (x > 0)
Theo đề ta có: (x + 2).5 = (x - 2).6
<=> 5x + 10 = 6x - 12
<=> 5x - 6x = -12 - 10
<=> -x = -22
<=> x = 22
AB dài: (22 + 2).5 = 120 (km)