Trong mặt phẳng tọa độ Oxy, tổng khoảng cách từ gốc tọa độ đến tất cả các đường tiệm cận của đồ thị hàm số y = log 2 2 x + 3 x - 1 bằng

![]()
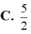
![]()
Tọa độ tất cả các điểm thuộc đồ thị (C) của hàm số y = x + 1 x - 2 sao cho tổng khoảng cách từ điểm đó đến 2 tiệm cận là nhỏ nhất là
A. (1;1)
B.![]()
C. ![]()
D. ![]()
Khoảng cách từ gốc tọa độ đến giao điểm của hai đường tiệm cận của đồ thị hàm số y = 2 x + 1 x + 1 bằng
A. 2 .
B. 5 .
C. 5.
D. 3 .
Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
A. -4
B. -5
C. -6.
D. -7
Ta có y’ = 3x2- 6mx + 3( m2-1).
Hàm số đã cho có cực trị thì phương trình y’ =0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nghiệm phân biệt ⇔ ∆ = 1 > 0 , ∀ m
Khi đó, điểm cực đại A( m-1; 2-2m) và điểm cực tiểu B( m+1; -2-2m)
Ta có
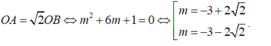
Tổng hai giá trị này là -6.
Chọn C.
tìm m để đồ thị hàm số y=(m-1)x+m+2 đi qua điểm M (1,2)với giá trị của m tìm được hãy tính khoảng cách từ gốc tọa độ O của mặt phẳng tọa độ Oxy đến đồ thì hàm số y=(m-1)x+m+2
a: Thay x=1 và y=2 vào (d), ta được:
2m+1=2
hay \(m=\dfrac{1}{2}\)
tìm m để đồ thị hàm số y=(m-1)x+m+2 đi qua điểm M (1,2)với giá trị của m tìm được hãy tính khoảng cách từ gốc tọa độ O của mặt phẳng tọa độ Oxy đến đồ thì hàm số y=(m-1)x+m+2
Thay x=1 và y=2 vào (d), ta được:
2m+1=2
hay \(m=\dfrac{1}{2}\)
cho các hàm số y+x-2 (d) và y+-0.5x+2(d') có đồ thị là các đườngthẳng:
a) hai hàm số ở trên, hàm số nào đồng biến, hàm số nào nghịch biến? vì sao?
b) vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của hai hàm số nói trên
c) tính khoảng cách từ gốc tọa độ O đến đường thẳng (d'): y+-0.5x+2
Tìm tọa độ điểm M có hoành độ dương thuộc đồ thị (C) của hàm số y = x + 2 x − 2 sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C) đạt giá trị nhỏ nhất.
A. M(1;-3)
B. M(3;5)
C. M(0;-1)
D. M(4;3)
Đáp án là D

Dấu “ = ” xảy ra ó
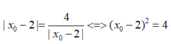
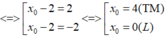
Vậy M(4;3)
Gọi M là điểm có hoành độ dương thuộc đồ thị hàm số y = x + 2 x − 2 sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất. Tọa độ điểm M là
A. 4 ; 3
B. 0 ; − 1
C. 1 ; − 3
D. 3 ; 5
Tọa độ điểm M có hoành độ dương thuộc đồ thị hàm số y = x + 2 x - 2 sao cho tổng khoảng cách từ M đến 2 tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất là
A.![]()
B. ![]()
C.![]()
D.![]()