Có bao nhiêu giá trị thực của tham số m để hàm số y = \(\left|x^2+mx+1\right|\) trên [-1;2] đạt giá trị nhỏ nhất bằng 1
Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số y=|x^2+2x+m-4| trên đoạn [-2;-1] bằng 4
Có bao nhiêu giá trị thực của tham số m để hàm số y = cos x + m . sin x + 1 cos x + 2 có giá trị lớn nhất bằng 1
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
Cho hàm số y = m sin x + 1 cos x + 2 . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5; 5] để giá trị nhỏ nhất của y nhỏ hơn -1
A. 6
B. 3
C. 4
D. 5
câu 19: Tìm giá trị thực của tham số m khác 0 để hàm số y= mx^2-2mx-3m-2 có giá trị nhỏ nhất bằng -10 trên R
câu 20: Gọi S là tập hợp tất cả giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y=f(x)=4x^2-4mx+m^2-2m trên đoạn [-2;0] bằng 3 . Tính tổng T các phần tử của S
Câu 38/Đề 7: Có bao nhiêu giá trị nguyên thuộc [-10;10] của m để giá trị lớn nhất của hàm số y=-x^4 +4x- m trên đoạn [-1;3] nhỏ hơn 10
Để tìm số giá trị nguyên của m trong khoảng [-10;10] sao cho giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3] nhỏ hơn 10, chúng ta cần thực hiện các bước sau:
1. Tìm giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3].
2. Kiểm tra xem giá trị lớn nhất của hàm số có nhỏ hơn 10 hay không.
3. Đếm số giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện trên.
Bước 1: Tìm giá trị lớn nhất của hàm số y = -x^4 + 4x - m trên đoạn [-1;3].
Để tìm giá trị lớn nhất, chúng ta có thể lấy đạo hàm của hàm số và giải phương trình đạo hàm bằng 0.
y' = -4x^3 + 4
Để tìm giá trị của x khi đạo hàm bằng 0, giải phương trình:
-4x^3 + 4 = 0
X^3 - 1 = 0
( x - 1)( x^2 + x + 1) = 0
Phương trình có 2 nghiệm: x = 1 và x^2 + x + 1 =0 (phương trình bậc 2).
Bước 2: Kiểm tra giá trị lớn nhất của hàm số có nhỏ hơn 10 hay không.
Để kiểm tra giá trị lớn nhất của hàm số, chúng ta có thể thay x = 1 vào hàm số:
y = - 1^4(1) - m = 3 - m
Điều kiện y < 10:
3 - m < 10
- m < 7
m > -7
Bước 3: Đếm số giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện trên.
Trong khoảng [-10;10], có 17 giá trị nguyên. Tuy nhiên, chúng ta chỉ quan tâm đến các giá trị m > -7.
Vậy, có 17 - 7 = 10 giá trị nguyên của m trong khoảng [-10;10] thỏa mãn điều kiện y < 10.
Để tiết kiệm vật liệu nhất thì S t p nhỏ nhất ⇔ πR 2 = π R ⇒ R = 1 ⇒ h = 2 Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây:
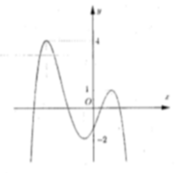
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x - 2 ) - m 4 có 7 điểm cực trị.
A. 1
B. 2
C. 3
D. 4
Có bao nhiêu giá trị nguyên dương của tham số m để giá trị nhỏ nhất của hàm số y = x + m 2 x - 1 trên đoạn [2;3] bằng 14.
A. 2
B. 1
C. 0
D. 4
Chọn B
Tập xác định D = ℝ \{1}
Ta có 
Do đó hàm số nghịch biến trên đoạn [2;3]
Suy ra 
Vậy có 1 giá trị nguyên dương của m.
