Cho biết ∫ 1 3 d x e x - 1 = a ln e 2 + e + 1 - 2 b với a, b là các số nguyên. Tính K = a + b
A. K = 2
B. K = 6
C. K = 5
D. K = 9
Bài 2 Tìm các số nguyên x,y biết :
c) (x-3).y=-14
d) (x-3).(y+4)=-7
e) (x-3).(y+4)=5
Bài 3 tìm x E Z sao cho
c) -19 là bội của x+3 d) x+5 là ước của x-2 e) 4x+1 chia hết cho x-1
cho P(x) = ax^4 +bx^3 +cx^2 +dx +e. tìm a, b ,c ,d ,e biết P(x) chia hết cho x^2 -1, chia cho x^2 +2 dư x P(2) = 2012
Cho S : x 2 + y 2 + z 2 = 3 và d : x - 1 2 = y + 1 - 2 = z - 1 . Biết d ∩ S = E , F . Tính EF.
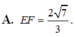
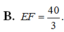
![]()

Cho S : x 2 + y 2 + z 2 = 3 và d : x - 1 2 = y + 1 - 2 = z - 1 . Biết d ∩ S = E , F . Tính EF.
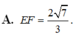
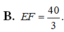
![]()
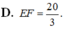
1.Tìm a,b,c,d,e\(\inℤ\) biết a + b + c + d + e = 0 và a + b = c + d = d + e = 2
2.Tìm x,y,z\(\inℤ\) biết :
a) x + y + z = 0, x + y = 3, y + z = -1
b) x + y = 3, y + z = 1, z + x = -2
1,Tìm các số tự nhiên a,b,c,d,e biết a<<c<d<e và 1/a+1/b+1/c+1/d+1/e=1
2,Tìm x thuộc N biết:
1/3+1/6+1/10+...+2/x.(x+1)=1999/2001
1.Tìm x biết
a,2^x=128 b,8^x-1=64
c,3+3^x=30 d,(x+2)=64
e,3^2.x=3^5 f,(2x-1^3)=343
Giải nhanh giúp mik vs mik sắp đi hc r ai nhanh mik tick cho
1.
a) \(2^x=128\)
\(2^x=2^7\)
\(=>x=7\)
b) \(8^{x-1}=64\)
\(8^{x-1}=8^2\)
\(=>x-1=2\)
\(x=2+1\)
\(=>x=3\)
c) \(3+3^x=30\)
\(3^x=30-3\)
\(3^x=27=3^3\)
\(=>x=3\)
d) \(\left(x+2\right)=64\) -> đề có thiếu không vậy?
e) \(3^2.x=3^5\)
\(x=3^5:3^2\)
\(=>x=3^3=27\)
f) \(\left(2x-1\right)^3=343\)
\(\left(2x-1\right)^3=7^3\)
\(=>2x-1=7\)
\(2x=7+1\)
\(2x=8\)
\(x=8:2\)
\(=>x=4\)
\(#Wendy.Dang\)
a,\(2^x\)=128 b,\(8^{x-1}\)=64 c,3+\(3^x\)=30 d,x+2=64
\(2^7\)=128 \(8^{x-1}\)=\(8^2\) \(3^x\)=30-3 x=64-2
=>x=7 =>x-1=2 \(3^x\)=27 x=62
x=2+1=3 \(3^x\)=\(3^3\)
=>x=3
e,\(3^2\).x=\(3^5\) f,(2x-\(1^3\))=343
x=\(3^5\):\(3^2\) 2x=1+343
x=27 2x=344
x=344:2
x=172
tìm x thuộc z biết:
a,4x-5 chia hết cho x
b,-11 chia hết cho (x-1)
c,(2x-2) chia hết cho (2x-1)
d,6(x-2)-3(x+1)=6
e,3(x-7)+2(x+1)=1
g,3(x-2)+5(x-3)-7x=-24
Cho biểu thức C =( \(\dfrac{2x^2+1}{x^3-1}-\dfrac{1}{x-1}\)):(1-\(\dfrac{x^2-2}{x^2+x+1}\))
a) Rút gọn C
b) Tính giá trị của C biết |1-x| +2 =3(x+1)
c) Tìm x nguyên để C nguyên
d) Tìm x biết |C| > C
e) Tìm x để C2-C + 1 đạt giá trị nhỏ nhất
\(C=\left(\dfrac{2x^2+1}{x^3-1}-\dfrac{1}{x-1}\right)\div\left(1-\dfrac{x^2-2}{x^2+x+1}\right)\)
ĐKXĐ: \(x\ne1\)
\(C=[\left(\dfrac{2x^2+1}{(x-1)\left(x^2+x+1\right)}-\dfrac{1}{x-1}\right)]\div\left(1-\dfrac{x^2-2}{x^2+x+1}\right)\)
\(\Leftrightarrow C=[\left(\dfrac{2x^2+1}{(x-1)\left(x^2+x+1\right)}-\dfrac{1\left(x^2+x+1\right)}{(x-1)\left(x^2+x+1\right)}\right)]\div[\dfrac{(x-1)\left(x^2+x+1\right)}{(x-1)\left(x^2+x+1\right)}-\dfrac{(x^2-2)(x-1)}{(x^2+x+1)\left(x-1\right)}]\)
\(\Rightarrow C=\left[2x^2+1-1\left(x^2+x+1\right)\right]\div\left[\left(x-1\right)\left(x^2+x+1\right)-\left(x-1\right)\left(x^2-2\right)\right]\)
\(\Rightarrow C=(2x^2+1-x^2-x-1)\div\left[\left(x-1\right)\left(x^2+x+1-x^2+2\right)\right]\)
\(\Rightarrow C=\left(x^2-x\right)\div\left[\left(x-1\right)\left(x+3\right)\right]\)
1.Cho biểu thức C=\(\frac{x+2}{x^2+x+1}-\frac{2}{x-1}-\frac{2x^2+4}{1-x^3}\)
a, Rút gọn C
b,So sánh C và \(\frac{1}{3}\)
2.Cho biểu thức D=\(\frac{3x}{x-3}-\frac{8x+3}{2x+1}-\frac{70}{2x^2-5x-3}\)
a, Rút gọn D
b, Tính giá trị của D biết |x+3|=7
c, Tìm x nguyên để D nguyên
3.Cho biểu thức E =\(\frac{x-1}{2}:\left(\frac{x^2+2}{x^3-1}-\frac{x}{x^2+x+1}+\frac{1}{1-x}\right)\)
a, Rút gọn E
b, Chứng minh rằng E> 0 với mọi x khác 1
C, Tìm giá trị nhỏ nhất của E